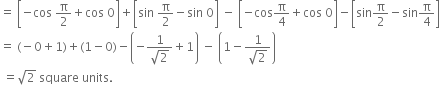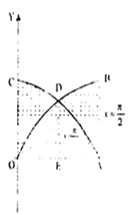Long Answer Type
Long Answer TypeFind the area bounded by the curve  y = x2 and the line y = x.
OR
Find the area of the region {(x. y): x2¬†‚ȧ y ‚ȧ x}.
Find the area of the region bounded by the line y = 3 x + 2, the x-axis and the ordinates x = - 1 and x = 1.
Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis.
OR
Draw the rough sketch and find the area of the region:
{(x, y): x2 < y < x + 2}
 Short Answer Type
Short Answer TypeDraw a rough sketch of the curves y = sin x and y = cos x as x varies from 0 to ![]()  and find the area of the region enclosed by them and the x-axis.
 and find the area of the region enclosed by them and the x-axis.
Let OB and CA represent the curves y = sin x and y = cos x as x varies from 0 to ![]() . The two curves intersect at D where
. The two curves intersect at D where
                                ![]()
Required area = Area OAB + area OCA - area ODA
                         ![]()
                          ![]()