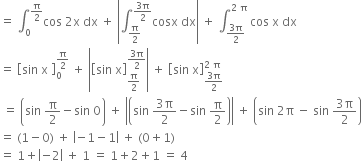Long Answer Type
Long Answer TypeFind the area bounded by the curve y = x2 and the line y = x.
OR
Find the area of the region {(x. y): x2 ≤ y ≤ x}.
Find the area of the region bounded by the line y = 3 x + 2, the x-axis and the ordinates x = - 1 and x = 1.
Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis.
OR
Draw the rough sketch and find the area of the region:
{(x, y): x2 < y < x + 2}
 Short Answer Type
Short Answer TypeDraw a rough sketch of the curves y = sin x and y = cos x as x varies from 0 to ![]() and find the area of the region enclosed by them and the x-axis.
and find the area of the region enclosed by them and the x-axis.
Find the area bounded by the curve y = cos x between x = 0 and x = 2 ![]() .
.
The equation of curve is
y = cos x
Its rough sketch from x = 0 to x = 2 ![]() is shown in figure.
is shown in figure.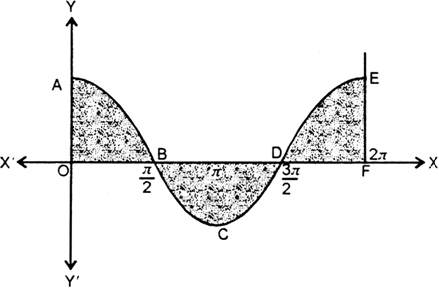
Required area = area of the region OABO + area of the region BCDB + area of the region DEFD.