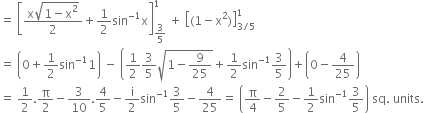Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeFind the area of the region bounded by the circle x2 + y2 = 1 and x + y = 1. Also draw a rough sketch.
Find the area of the region {(x, y): x2 ≤ y ≤ |x|}.
Or
Find the area of the region bounded by the parabola y = x2 and y = |x|.
We are able to find the area included between the curves
![]() ...(1)
...(1)
and ![]() ...(2)
...(2)
From (1) and (2), we get,
![]()
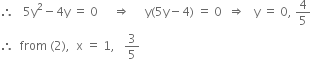
![]() circle (1) and line (2) intersect in points A (1, 0) and
circle (1) and line (2) intersect in points A (1, 0) and ![]()
Required area is shaded.
Required area = ![]()