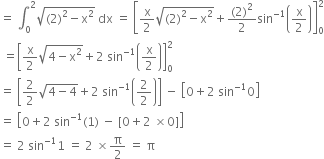Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Integrals

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Long Answer Type

71. Draw a rough sketch of the region {(x, y): y² ≤ 3 x, 3 x² + 3 y² ≤ 16} and find the area enclosed by the region using method of integration.

111 Views

72.

Find the area of the smaller part of the circle x² + y² = a cut oil by the line $straight x equals fraction numerator straight a over denominator square root of 2 end fraction$

135 Views

73. Find the area of the smaller region bounded by the ellipse

straight x squared over 9 plus straight y squared over 4 space equals space 1

and the straight line

straight x over 3 plus straight y over 2 space equals space 1

386 Views

74.

Using integration, find the area of the smaller region bounded by the curve $straight x squared over 16 plus straight y squared over 9 space equals space 1$ and the straight line $straight x over 4 plus straight y over 3 equals 1.$

138 Views

75.

Find the area of smaller region bounded by the ellipse $straight x squared over straight a squared plus straight y squared over straight b squared space equals 1$ and the straight line $straight x over straight a plus straight y over straight b equals 1$

110 Views

76. Evaluate

integral subscript 0 superscript straight r square root of straight r squared minus straight x squared end root dx

, where x is a fixed positive number, Hence, prove that the area of a circle of radius r is

straight pi space straight r squared.

97 Views

Short Answer Type

77.

Find the whole area of the circle x² + y² = a².

350 Views

Multiple Choice Questions

78. Area lying in the first quadrant and bounded by the circle x² + y² = 4 and the lines x = 0 and x = 2 is
$straight pi$
$straight pi over 2$
$straight pi over 3$
$straight pi over 3$

straight pi

The equation of circle is
$straight x squared plus straight y squared space equals space 4$ ...(1)
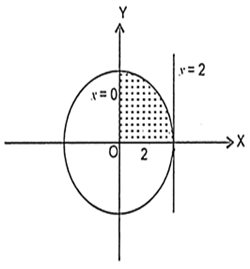
We are to find the area of the circle lying between the lines x = 0 and x = 2 in the first quadrant.
Required area = $integral subscript 0 superscript 2 straight y space dx$
$equals space integral subscript 0 superscript 2 square root of 4 minus straight x squared space end root dx$ $open square brackets because space space space of space left parenthesis 1 right parenthesis close square brackets$

$equals space integral subscript 0 superscript 2 square root of left parenthesis 2 right parenthesis squared minus straight x squared end root space dx space equals space open square brackets straight x over 2 square root of left parenthesis 2 right parenthesis squared minus straight x squared end root plus fraction numerator left parenthesis 2 right parenthesis squared over denominator 2 end fraction sin to the power of negative 1 end exponent open parentheses straight x over 2 close parentheses close square brackets subscript 0 superscript 2 space equals open square brackets straight x over 2 square root of 4 minus straight x squared end root plus 2 space sin to the power of negative 1 end exponent open parentheses straight x over 2 close parentheses close square brackets subscript 0 superscript 2 equals space open square brackets 2 over 2 square root of 4 minus 4 end root plus 2 space sin to the power of negative 1 end exponent open parentheses 2 over 2 close parentheses close square brackets space minus space open square brackets 0 plus 2 space sin to the power of negative 1 end exponent 0 close square brackets equals space open square brackets 0 plus 2 space sin to the power of negative 1 end exponent left parenthesis 1 right parenthesis space minus space left square bracket 0 plus 2 space cross times 0 right square bracket close square brackets equals space 2 space sin to the power of negative 1 end exponent 1 space equals space 2 space cross times straight pi over 2 space equals space straight pi$

221 Views

79. Area of the region bounded by the curve y² = 4 x, y-axis and the line y = 3 is

2
$9 over 4$
$9 over 3$
$9 over 3$

107 Views

80. Smaller area enclosed by the circle x² + y² = 4 and the line x + y = 2 is
Choose the correct answer.
or
Draw the rough sketch and find the area of the region:
{(x, y): x² + y² < 4, x + y > 2}.