Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Integrals

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

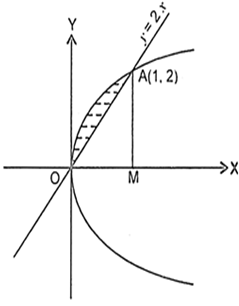
Multiple Choice Questions

81.
Area lying between the curves y² = 4x and y = 2x is

$2 over 3$
$1 third$
$1 fourth$
$1 fourth$

1 third

The equations of the curves are
$straight y squared space equals space 4 straight x$ ...(1)
and    $straight y equals space 2 straight x$ ...(2)
From (1) and (2),
   $4 straight x squared space equals space 4 straight x$
or    $4 straight x left parenthesis straight x minus 1 right parenthesis space equals space 0$ .

$therefore space space space space space space space space space straight x space equals space 0 comma space space 1 therefore space space space from space left parenthesis 2 right parenthesis comma space space straight y space equals space 0 comma space 2 therefore space space space curves space left parenthesis 1 right parenthesis space and space left parenthesis 2 right parenthesis space intersect space in space straight O left parenthesis 0 comma space 0 right parenthesis comma space space space straight A left parenthesis 6 comma space 2 right parenthesis$

Required area = 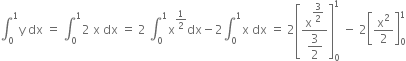$integral subscript 0 superscript 1 straight y space dx space equals space integral subscript 0 superscript 1 2 space straight x space dx space equals space 2 space integral subscript 0 superscript 1 straight x to the power of 1 half end exponent dx minus 2 integral subscript 0 superscript 1 straight x space dx space equals space 2 open square brackets fraction numerator straight x to the power of begin display style 3 over 2 end style end exponent over denominator begin display style 3 over 2 end style end fraction close square brackets subscript 0 superscript 1 space minus space 2 open square brackets straight x squared over 2 close square brackets subscript 0 superscript 1$
$equals space 4 over 3 open square brackets straight x to the power of 3 over 2 end exponent close square brackets subscript 0 superscript 1 space minus space open square brackets straight x squared close square brackets subscript 0 superscript 1 space equals space 4 over 3 left parenthesis 1 minus 0 right parenthesis minus space left parenthesis 1 minus 0 right parenthesis space equals space 4 over 3 minus 1 space equals space 1 third$

196 Views

82. Area bounded by the curve y = x³ the x-axis and the ordinates x - 2 and a = 1 is

-9
$fraction numerator negative 15 over denominator 4 end fraction$
$15 over 4$
$15 over 4$

110 Views

83. The area bounded by the curve y = x |x|, x-axis and the ordinates x = - 1 and x = 1 is given by

0
$1 third$
$2 over 3$
$2 over 3$

122 Views

84. The area of the circle x +y =16 exterior to the parabola y² = 6x is

$4 over 3 left parenthesis 4 straight pi minus square root of 3 right parenthesis$
$4 over 3 left parenthesis 4 straight pi plus square root of 3 right parenthesis$
$4 over 3 left parenthesis 8 straight pi minus square root of 3 right parenthesis$
$4 over 3 left parenthesis 8 straight pi minus square root of 3 right parenthesis$

196 Views

85.

The area bounded by the x-axis, y = cosx and y = sin x when $0 less or equal than straight x less or equal than straight pi over 2$

$2 left parenthesis square root of 2 minus 1 right parenthesis$
$square root of 2 minus 1$
$square root of 2 plus 1$
$square root of 2 plus 1$

162 Views

Long Answer Type

86. Prove that the curves y² = 4x and x² = 4y divide the area of the square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.

640 Views

87.

Using the method of integration, find the area of the triangular region whose vertices are (2, -2), (4, 3) and (1, 2).

1133 Views

88.

Sketch the region bounded by the curves $straight y equals square root of 5 minus straight x squared end root space and space straight y space equals open vertical bar straight x minus 1 close vertical bar$ and find its area using integration.