Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Integrals

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Multiple Choice Questions

81.

Area lying between the curves y² = 4x and y = 2x is

$2 over 3$
$1 third$
$1 fourth$
$1 fourth$

196 Views

82. Area bounded by the curve y = x³ the x-axis and the ordinates x - 2 and a = 1 is

-9
$fraction numerator negative 15 over denominator 4 end fraction$
$15 over 4$
$15 over 4$

110 Views

83. The area bounded by the curve y = x |x|, x-axis and the ordinates x = - 1 and x = 1 is given by

0
$1 third$
$2 over 3$
$2 over 3$

122 Views

84. The area of the circle x +y =16 exterior to the parabola y² = 6x is

$4 over 3 left parenthesis 4 straight pi minus square root of 3 right parenthesis$
$4 over 3 left parenthesis 4 straight pi plus square root of 3 right parenthesis$
$4 over 3 left parenthesis 8 straight pi minus square root of 3 right parenthesis$
$4 over 3 left parenthesis 8 straight pi minus square root of 3 right parenthesis$

196 Views

85.
The area bounded by the x-axis, y = cosx and y = sin x when $0 less or equal than straight x less or equal than straight pi over 2$

$2 left parenthesis square root of 2 minus 1 right parenthesis$
$square root of 2 minus 1$
$square root of 2 plus 1$
$square root of 2 plus 1$

square root of 2 minus 1

The two curves y = sin x and y = cos x meet where sin x = cos x , i.e., where x = 1
$rightwards double arrow space space space space straight x space equals space straight pi over 4.$
Required area (show shaded)
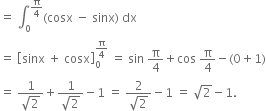
$equals space integral subscript 0 superscript straight pi over 4 end superscript left parenthesis cosx space minus space sinx right parenthesis space dx equals space open square brackets sinx space plus space cosx close square brackets subscript 0 superscript straight pi over 4 end superscript space equals space sin space straight pi over 4 plus cos space straight pi over 4 minus left parenthesis 0 plus 1 right parenthesis equals space fraction numerator 1 over denominator square root of 2 end fraction plus fraction numerator 1 over denominator square root of 2 end fraction minus 1 space equals space fraction numerator 2 over denominator square root of 2 end fraction minus 1 space equals space square root of 2 minus 1.$

162 Views

Long Answer Type

86. Prove that the curves y² = 4x and x² = 4y divide the area of the square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.

640 Views

87.

Using the method of integration, find the area of the triangular region whose vertices are (2, -2), (4, 3) and (1, 2).

1133 Views

88.

Sketch the region bounded by the curves $straight y equals square root of 5 minus straight x squared end root space and space straight y space equals open vertical bar straight x minus 1 close vertical bar$ and find its area using integration.