Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Integrals

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Multiple Choice Questions

81.

Area lying between the curves y² = 4x and y = 2x is

$2 over 3$
$1 third$
$1 fourth$
$1 fourth$

196 Views

82. Area bounded by the curve y = x³ the x-axis and the ordinates x - 2 and a = 1 is

-9
$fraction numerator negative 15 over denominator 4 end fraction$
$15 over 4$
$15 over 4$

110 Views

83. The area bounded by the curve y = x |x|, x-axis and the ordinates x = - 1 and x = 1 is given by

0
$1 third$
$2 over 3$
$2 over 3$

122 Views

84. The area of the circle x +y =16 exterior to the parabola y² = 6x is

$4 over 3 left parenthesis 4 straight pi minus square root of 3 right parenthesis$
$4 over 3 left parenthesis 4 straight pi plus square root of 3 right parenthesis$
$4 over 3 left parenthesis 8 straight pi minus square root of 3 right parenthesis$
$4 over 3 left parenthesis 8 straight pi minus square root of 3 right parenthesis$

196 Views

85.

The area bounded by the x-axis, y = cosx and y = sin x when $0 less or equal than straight x less or equal than straight pi over 2$

$2 left parenthesis square root of 2 minus 1 right parenthesis$
$square root of 2 minus 1$
$square root of 2 plus 1$
$square root of 2 plus 1$

162 Views

Long Answer Type

86. Prove that the curves y² = 4x and x² = 4y divide the area of the square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.

The equation of curves are
   $straight y squared space equals space 4 straight x$ ...(1)
and $straight x squared space equals space 4 straight y$ ...(2)
From (2), $straight y equals straight x squared over 4$ ...(3)
Putting this value of y in (1),
$straight x to the power of 4 over 16 space equals space 4 straight x space space space or space space straight x to the power of 4 space equals space 64 straight x$
or    $straight x left parenthesis straight x cubed minus 64 right parenthesis space equals space 0$
$therefore space space space space straight x space equals space 0 comma space 4 therefore space space space from space left parenthesis 3 right parenthesis comma space space straight y space equals space 0 comma space space 4 because space space space curves space left parenthesis 1 right parenthesis space and space left parenthesis 2 right parenthesis space intersect space in space straight O left parenthesis 0 comma space 0 right parenthesis comma space straight P left parenthesis 4 comma space 4 right parenthesis$

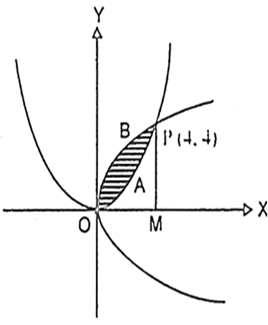
From P. draw PM ⊥ x-axis.
Required area = Area OAPB = Area OBPM - area OAPM
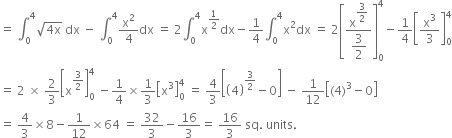
   $equals space integral subscript 0 superscript 4 square root of 4 straight x end root space dx space minus space integral subscript 0 superscript 4 straight x squared over 4 dx space equals space 2 integral subscript 0 superscript 4 straight x to the power of 1 half end exponent dx minus 1 fourth integral subscript 0 superscript 4 straight x squared dx space equals space 2 open square brackets fraction numerator straight x to the power of begin display style 3 over 2 end style end exponent over denominator begin display style 3 over 2 end style end fraction close square brackets subscript 0 superscript 4 minus 1 fourth open square brackets straight x cubed over 3 close square brackets subscript 0 superscript 4 equals space 2 space cross times space 2 over 3 open square brackets straight x to the power of 3 over 2 end exponent close square brackets subscript 0 superscript 4 space minus 1 fourth cross times 1 third open square brackets straight x cubed close square brackets subscript 0 superscript 4 space equals space 4 over 3 open square brackets open parentheses 4 close parentheses to the power of 3 over 2 end exponent minus 0 close square brackets space minus space 1 over 12 open square brackets left parenthesis 4 right parenthesis cubed minus 0 close square brackets equals space 4 over 3 cross times 8 minus 1 over 12 cross times 64 space equals space 32 over 3 minus 16 over 3 equals space 16 over 3 space sq. space units.$
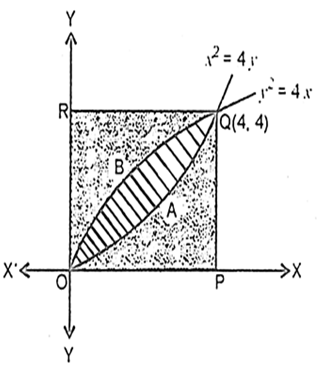
Now, the area of the region OAQBO bounded by curves $straight y squared space equals 4 straight x$ and $straight x squared space equals space 4 straight y$

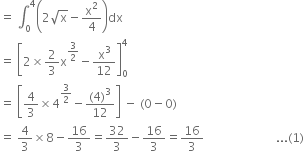
$equals space integral subscript 0 superscript 4 open parentheses 2 square root of straight x minus straight x squared over 4 close parentheses dx equals space open square brackets 2 cross times 2 over 3 straight x to the power of 3 over 2 end exponent minus straight x cubed over 12 close square brackets subscript 0 superscript 4 equals space open square brackets 4 over 3 cross times 4 to the power of 3 over 2 end exponent minus fraction numerator left parenthesis 4 right parenthesis cubed over denominator 12 end fraction close square brackets space minus space left parenthesis 0 minus 0 right parenthesis equals space 4 over 3 cross times 8 minus 16 over 3 equals 32 over 3 minus 16 over 3 equals 16 over 3 space space space space space space space space space space space space space space space space space space space space space space space space... left parenthesis 1 right parenthesis$

Again, the area of the region OPQAO bounded by the curves x² = 4 y, x = 0, x = 4 and x-axis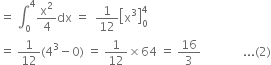
$equals space integral subscript 0 superscript 4 straight x squared over 4 dx space equals space space 1 over 12 open square brackets straight x cubed close square brackets subscript 0 superscript 4 equals space 1 over 12 left parenthesis 4 cubed minus 0 right parenthesis space equals space 1 over 12 cross times 64 space equals space 16 over 3 space space space space space space space space space space space space space space... left parenthesis 2 right parenthesis$
Similarly, the area of the region OBQRO bounded by the curve $straight y squared space equals space 4 straight x comma space space straight y space equals space 0 space space and space space straight y space equals 4$
$equals space integral subscript 0 superscript 4 space straight x space dy space equals space integral subscript 0 superscript 4 straight y squared over 4 dy space equals space 1 over 12 open square brackets straight y cubed close square brackets subscript 0 superscript 4 space equals space 16 over 3$ ...(3)
From (1), (2) and (3), it is clear that the area of the region OAQBO = area of the region OPQAO = area of the region OBQRO, i.e., urea bounded by parabolas y² = 4 x and x² = 4 y divides the area of the square in three equal parts.

640 Views

87.

Using the method of integration, find the area of the triangular region whose vertices are (2, -2), (4, 3) and (1, 2).

1133 Views

88.

Sketch the region bounded by the curves $straight y equals square root of 5 minus straight x squared end root space and space straight y space equals open vertical bar straight x minus 1 close vertical bar$ and find its area using integration.

600 Views

89.

Using integration, find the area of the region bounded by the triangle whose vertices are (-1, 2), (1, 5) and (3, 4).

363 Views

90.

Using integration, find the area bounded by the curve x² = 4y and the line x = 4y – 2.

350 Views