Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Integrals

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Multiple Choice Questions

81.

Area lying between the curves y² = 4x and y = 2x is

$2 over 3$
$1 third$
$1 fourth$
$1 fourth$

196 Views

82. Area bounded by the curve y = x³ the x-axis and the ordinates x - 2 and a = 1 is

-9
$fraction numerator negative 15 over denominator 4 end fraction$
$15 over 4$
$15 over 4$

110 Views

83. The area bounded by the curve y = x |x|, x-axis and the ordinates x = - 1 and x = 1 is given by

0
$1 third$
$2 over 3$
$2 over 3$

122 Views

84. The area of the circle x +y =16 exterior to the parabola y² = 6x is

$4 over 3 left parenthesis 4 straight pi minus square root of 3 right parenthesis$
$4 over 3 left parenthesis 4 straight pi plus square root of 3 right parenthesis$
$4 over 3 left parenthesis 8 straight pi minus square root of 3 right parenthesis$
$4 over 3 left parenthesis 8 straight pi minus square root of 3 right parenthesis$

196 Views

85.

The area bounded by the x-axis, y = cosx and y = sin x when $0 less or equal than straight x less or equal than straight pi over 2$

$2 left parenthesis square root of 2 minus 1 right parenthesis$
$square root of 2 minus 1$
$square root of 2 plus 1$
$square root of 2 plus 1$

162 Views

Long Answer Type

86. Prove that the curves y² = 4x and x² = 4y divide the area of the square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.

640 Views

87.

Using the method of integration, find the area of the triangular region whose vertices are (2, -2), (4, 3) and (1, 2).

1133 Views

88.

Sketch the region bounded by the curves $straight y equals square root of 5 minus straight x squared end root space and space straight y space equals open vertical bar straight x minus 1 close vertical bar$ and find its area using integration.

600 Views

89.

Using integration, find the area of the region bounded by the triangle whose vertices are (-1, 2), (1, 5) and (3, 4).

363 Views

90.
Using integration, find the area bounded by the curve x² = 4y and the line x = 4y – 2.

The shaded area OBAO represents the area bounded by the curve x² = 4y and the line x = 4y – 2.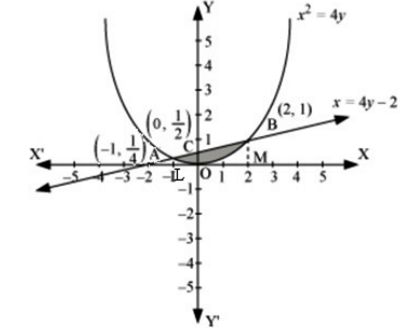

Let A and B be the points of intersection of the line and parabola.
Co-ordinates of point A are 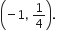$open parentheses negative 1 comma space 1 fourth close parentheses. space$ Co-ordinates of point B are (2, 1).
Area OBAO = Area OBCO + Area OACO ...(1)
Area OBCO =
$equals integral subscript 0 superscript 2 fraction numerator straight x plus 2 over denominator 4 end fraction dx minus integral subscript 0 superscript 2 straight x squared over 4 dx equals 1 fourth open square brackets straight x squared over 2 plus 2 straight x close square brackets subscript 0 superscript 2 minus 1 fourth open square brackets straight x cubed over 3 close square brackets subscript 0 superscript 2 equals 1 fourth open square brackets 2 plus 4 close square brackets minus 1 fourth open square brackets 8 over 3 close square brackets equals 3 over 2 minus 2 over 3 equals 5 over 6$
Area OACO =
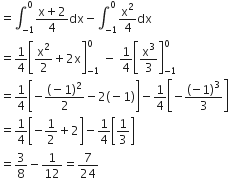
$equals integral subscript negative 1 end subscript superscript 0 fraction numerator straight x plus 2 over denominator 4 end fraction dx minus integral subscript negative 1 end subscript superscript 0 straight x squared over 4 dx equals 1 fourth open square brackets straight x squared over 2 plus 2 straight x close square brackets subscript negative 1 end subscript superscript 0 space minus space 1 fourth open square brackets straight x cubed over 3 close square brackets subscript negative 1 end subscript superscript 0 equals 1 fourth open square brackets negative fraction numerator left parenthesis negative 1 right parenthesis squared over denominator 2 end fraction minus 2 left parenthesis negative 1 right parenthesis close square brackets minus 1 fourth open square brackets negative open parentheses negative 1 close parentheses cubed over 3 close square brackets equals 1 fourth open square brackets negative 1 half plus 2 close square brackets minus 1 fourth open square brackets 1 third close square brackets equals 3 over 8 minus 1 over 12 equals 7 over 24$
Therefore, required area = $open parentheses 5 over 6 plus 7 over 24 close parentheses space equals 9 over 8 sq. units$