Using integration, find the area of the region enclosed between the two circles:

Find the area bounded by the circle x² + y² = 16 and the line √3y=x in the first quadrant, using integration.

Using integration, find the area of region bounded by the triangle whose vertices are (–2, 1), (0, 4) and (2, 3).

Using integration, find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x² + y² =32

Using integration find the area of the region bounded by the parabola y² = 4x and the circle 4x² + 4y² = 9.

Prove that the curves y²= 4x and x²= 4y divide the area of the square bonded by x = 0, x = 4, y = 4, and y = 0 into three equal parts.

Using integration, find the area of the following region:

$\left\{ \left( \mathrm{x}, \mathrm{y} \right): \frac{{\mathrm{x}}^2}{9} + \frac{{\mathrm{y}}^2}{4} \le 1 \le \frac{\mathrm{x}}{3} + \frac{\mathrm{y}}{2} \right\}$

98.

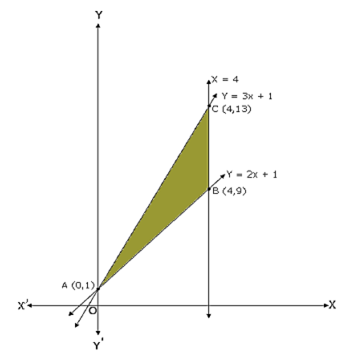
Using integration find the area of the triangular region whose sides have equations  y=2x+1,  y=3x+1  and  x=4.

Using the method of method of integration, find the area of the region bounded by the following lines:

3x – y – 3 = 0,

2x + y – 12 = 0,

x – 2y – 1 = 0

The area (in sq. units) enclosed between the curves y = x² and y = $\left|\mathrm{x}\right|$ is

• $\frac{2}{3}$

• $\frac{1}{6}$

• $\frac{1}{3}$

• 1