 Long Answer Type
Long Answer Type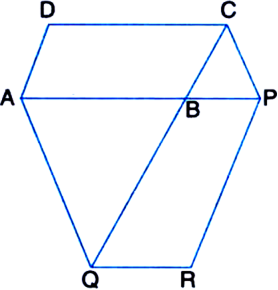
 Short Answer Type
Short Answer TypeIn figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar(ΔACB) = ar(ΔACF)
(ii) ar(□AEDF) = ar(ABCDE). 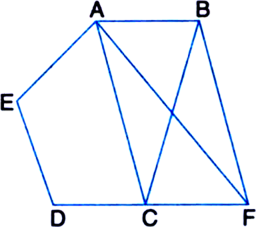
Show that the area of a rhombus is half the product of the lengths of its diagonals.
Or
Prove that the area of a rhombus is equal to half the rectangle contained by its diagonals.
Let ABCD be a rhombus whose diagonals are AC and BD.
Then,
Area of rhombus ABCD
= Area of ΔABD + Area of ΔCBD![]()
∵ Diagonals of a rhombus are perpendiculars to each other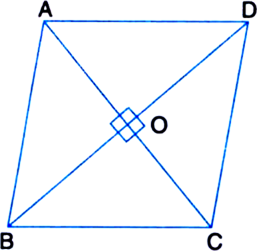
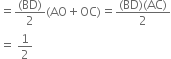
Product of the lengths of its diagonals.
