Short Answer TypeIn a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g., a section of Class I will plant 1 tree, a section of Class II will plant 2 trees and so on till Class XII. There are three sections of each class. How many trees will be planted by the students?
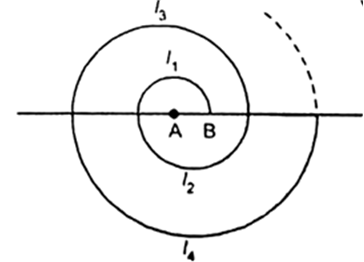
A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, . . . as shown in Fig. 5.4. What is the total length of such a spiral made up of thirteen consecutive semicircles? 
Long Answer Type
In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see the given Fig.)
A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?
Short Answer TypeWhich term of the AP : 121, 117, 113, . . ., is its first negative term? [Hint : Find n for an < 0]
Long Answer TypeThe sum of the third and the seventh terms of an AP is 6 and their product is 8. Find the sum of first sixteen terms of the AP.
Short Answer TypeA ladder has rungs 25 cm apart. (see the given Fig.). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and the bottom rungs are 
apart, what is the length of the wood required for the rungs?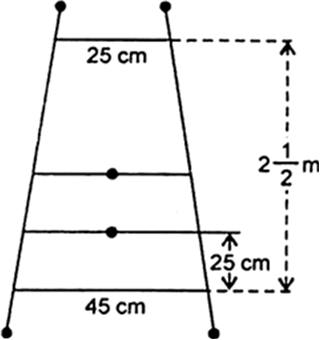
Long Answer TypeThe houses of a row are numbered consecutively from 1 to 49. Show that there is a value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to the sum of the numbers of the houses following it. Find this value of x.
m and a tread of 
m. (see the Fig.). Calculate the total volume of concrete required to build the terrace.
Short Answer TypeWhich of the following list of numbers does form an A .P. ? If they form an A .P., write the next two terms.
(i) 6, 1, –4, –9, –14............
(ii) 1, –3, –5...........
(iii) –2. 2. –2, 2, –2.............
(iv) 1, 1, 1, 2, 2, 3, 3,.............
(i) a2 – a1 = 1 – 6 = –5
a3 – a2 = –4 – 1 = –5
a4 – a3 = –9 – (–4) = –9 + 4 = –5
And, a5 – a3 = –14 – (–9) = –14 + 9 = 5
Since, the difference between each pair of consecutive terms are constant.
So, the given numbers form an A.P. with the common difference -5.
The next two terms are :
–14 + (–5) = –14 – 5 = –19
–19 + (–5) = –24.
(ii) a2 – a1 = –1 – 1 = –2
a3 – a2 = –3 – (–1) = –3 + 1 = –2
a4 – a3 = –5 – (–3) = –5 + 3 = –2
Since, the difference between each pair of consecutive terms are constant.
So, the given numbers form an A .P. with the common difference -2.
The next two terms are :
–5 + (–2) = –5 – 2 = –7
–7 + (–2) = –7 – 2 = –9.
(iii) a2 – a1 = 2 – (–2) = 2 + 2 = 4
a3 –a2 = –2 – (2) = –2 – 2 = –4
a4 – a3 = –5 – (–3) = –5 + 3 = –2
Since, the difference between each pair of consecutive terms are not constant.
So, the given numbers does not form an A .P.
(iv) a2 – a, = 1 – 1 = 0
a3 – a2 = 1 – 1 = 0
a4 – a3 = 2 – 1 = 1
a5 = 2 – 2 = 0
a6 – a5 = 3 – 2 = 1
a7 – a6 = 3 – 3 = 0
Since, the difference between each pair of consecutive term are not constant.
So, the given numbers does not form an A .P
Switch
