Short Answer TypeIf Sn, the sum of first n terms of an A .P. is given by Sn = 5n2 + 3n, then find its nthterm.
Sn = 5n2 + 3n
Find the sum of the :
(i) First 25 terms of an A .P. whose nth term is given by an= 7 – 3n
We have that,
an = 7 – 3n
If n = 1, a1 = 7 – 3n
= 7 – 3 = 4
n = 2, a2 = 7 – 3(2)
= 7 – 6 = 1
n = 3, = 7 – 3(3)
= 7 – 9 = –2
n = 4, a4 = 7 – 3(4)
= 7 – 12 = –5
So, we have following A .P.’s 4, 1, – 2, – 5, ..........
Here, a = 4, d = –3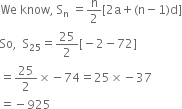
Hence, the sum of first 25 terms of an A .P.
be –925.
Long Answer TypeIf in sin A .P. the sum of m terms is equal to n and the sum of n terms is equal to m, then prove that the sum of (m + n) terms is –(m + n).
Switch
