Short Answer Type
Short Answer Type
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.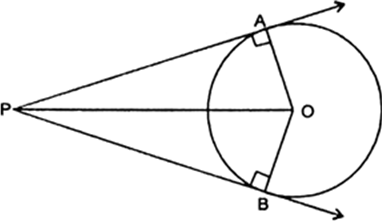
 Long Answer Type
Long Answer TypeA triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig. 10.14). Find the sides AB and AC. 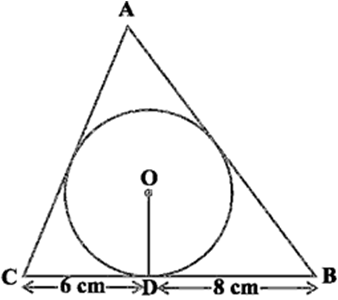
Fig, 10.14
Let O be the incentre of ΔABC such that
OD = OE = OF = 4 cm.
Also, BD = 6 cm, CD = 8 cm.
Since, length of tangents drawn from an external point are equal. 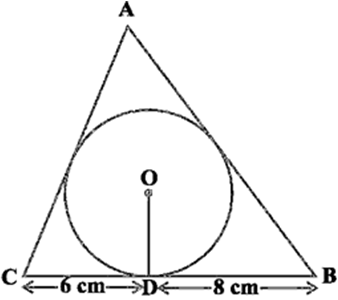
Fig. 10.14
So, BD = BF = 6 cm
and, CD = CE = 8 cm
Let the length of tangents drawn from first vertex be x.
⇒ AF = AE = x
[Tangents from external point A]
Now, sides of triangle arc
AB = x + 6 = c
BC = 6 + 8 = 14 = a
and AC = x + 8 = b
We know that : S = ![]()
![]() S =
S = ![]()
![]() S =
S = ![]()
Therefore,
Area of ΔABC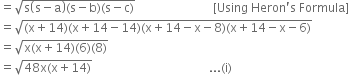
Also, area of ![]() ABC,
ABC,
= Area of ![]() BOC + Area of
BOC + Area of ![]() AOC +
AOC + ![]() AOB
AOB ![]()
![]()
= 28 + 2 (x + 8) + 2 (x + 6)
= 28 + 2x + 16 + 2x + 12
= 4x + 56 ...(ii)
Comparing (i) and (ii), we get
![]()
Squaring both sides, we get
48x (x + 14) = (4x + 56 )2 ![]() 48x (x + 14) = (4 (x + 14)]2
48x (x + 14) = (4 (x + 14)]2 ![]() 48x (x + 14) = 16 (x + 14)]2
48x (x + 14) = 16 (x + 14)]2 ![]() 3x (x + 14) = (x + 14)2
3x (x + 14) = (x + 14)2 ![]() 3x (x + 14) - (x + 14)2 = 0
3x (x + 14) - (x + 14)2 = 0![]() (x + 14) [3x - (x + 14)] = 0
(x + 14) [3x - (x + 14)] = 0![]() 3x - x - 14 = 0
3x - x - 14 = 0![]() 2x - 14 = 0
2x - 14 = 0![]() 2x = 14
2x = 14![]() x = 7
x = 7
Hencem AB = x + 6
= 7 + 6 = 13 cm
and AC = x + 8
= 7 + 8 = 15 cm.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
 Short Answer Type
Short Answer Type