Short Answer Type
Short Answer Type
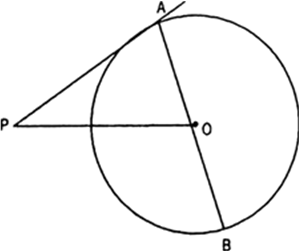
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.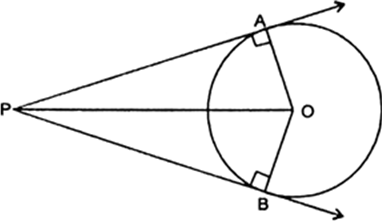
 Long Answer Type
Long Answer TypeA triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig. 10.14). Find the sides AB and AC. ┬Ā ┬Ā ┬Ā ┬Ā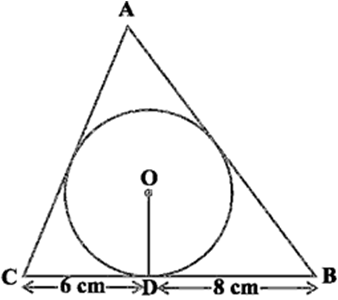 ┬Ā
┬Ā
Fig, 10.14
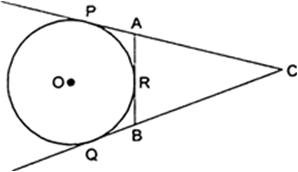
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
 Short Answer Type
Short Answer Type
Therefore, ŌłĀOPO =90┬░
It is given that PQ =15 cm
and ┬Ā┬Ā┬ĀOQ = 17 cm
In right ΔOPQ
OQ2┬Ā= OP2┬Ā+ PQ2
[Using Pythagoras theorem]
ŌćÆ (17)2┬Ā= OP2┬Ā+ (15)2
OP2┬Ā= (17)2┬ĀŌĆō (15)2
= 289 ŌĆō 225 = 64 ŌćÆ OP = 8 cm
Hence, radius of the circle = 8 cm.