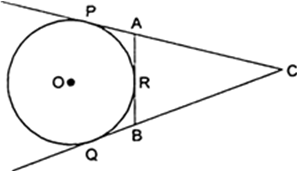
Short Answer Type
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.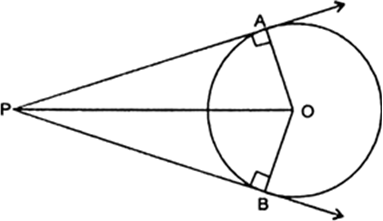
Long Answer TypeA triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig. 10.14). Find the sides AB and AC.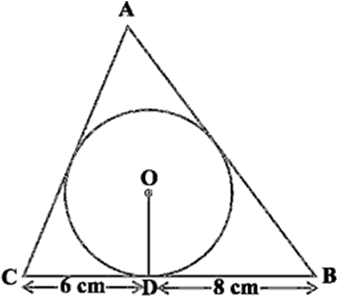 
Fig, 10.14
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Short Answer Type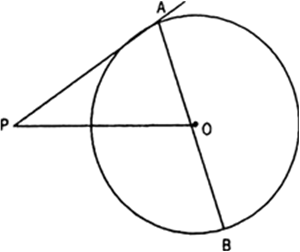
∠AOP + ∠POB = 180° [Linear pair]
⇒ ∠AOP + 115 = 180
⇒ ∠AOP = 180 – 115
= 65° ∠AOP = 90
[Line drawn through the centre to point of contact]
Now, In ΔAPO,
∠OAP + ∠AOP + ∠APO = 180
⇒ 90 + 65 + ∠APO = 180
⇒ ∠APO = 180 – 155
= 25°.
Switch
