 Short Answer Type
Short Answer Type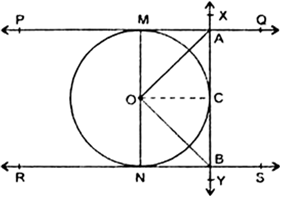
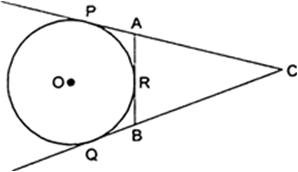
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.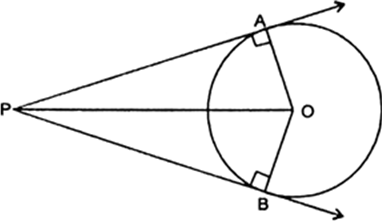
 Long Answer Type
Long Answer TypeA triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig. 10.14). Find the sides AB and AC. 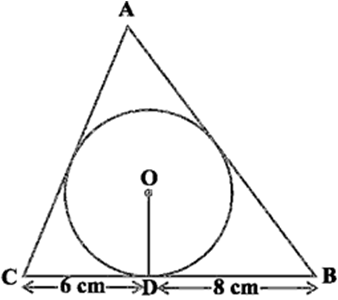
Fig, 10.14
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
 Short Answer Type
Short Answer Type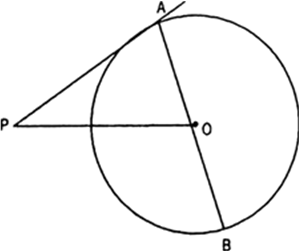
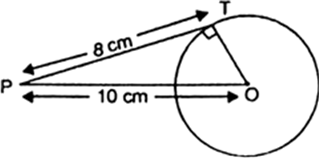
We know that, A line drawn through the centre to the point of contact is perpendicular on it.
∠OTP = 90°
Now, in right ΔOPT
OP2 = OT2 + PT2 (10)2 = OT2 + (8)2
⇒ 100 = OT2 + 64
⇒ OT2 = 100 – 64
⇒ OT2 = 30
⇒ OT = 6 cm
Hence, Radius of the circle is 6 cm.
