Short Answer Type
Short Answer Type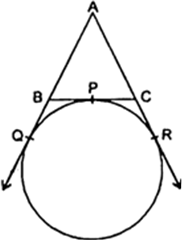
 Long Answer Type
Long Answer TypeSo, BP = BQ
(Tangents from external point B)
But BP = 27 cm
⇒ BQ = 27 cm
It is given that BC = 38 cm
⇒ BQ + CQ = 38
⇒ 27 + CQ = 38
⇒ CQ = 11 cm
⇒ CQ = CR (Tagents from an external point C)
But CQ = 11 cm
⇒ CR = 11 cm
It is given that : CD = 25 cm
⇒ CR + DR = 25
⇒ 11 + DR = 25
⇒ DR = 14 cm
Since, tangent to a circle is perpendicular to the radius through the point of contact.
∴ ∠ORD = ∠OSD = 90°
It is given that
∠D = 90°
Now, in quadrilateral ORDS,
∠ORD = ∠OSD = ∠RDS = ∠ROS = 90°
and OR = OS [radii of circle]
Therefore, ORDS is a square
So, OR = DR = 14 cm
Hence r = 14 cm.
 Short Answer Type
Short Answer Type
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer TypeFrom a point P outside a circle, with centre O tangents PA and PB are drawn as shown in the figure, prove that
(i) ⇒AOP = ∠BOP
(ii) OP is the perpendicular bisector of AB.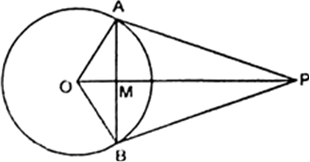
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type