Short Answer Type
Short Answer Type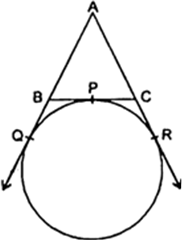
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type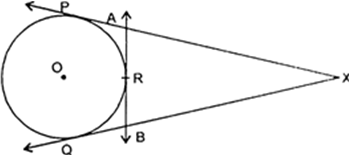
So, XP = XQ
AP = AR
and BQ = BR
Now XP = XQ
⇒ XA + AP = XB + BQ
⇒ XA + AR = XB + BR
[∵ AP = AR, BP = BR]
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer TypeFrom a point P outside a circle, with centre O tangents PA and PB are drawn as shown in the figure, prove that
(i) ⇒AOP = ∠BOP
(ii) OP is the perpendicular bisector of AB.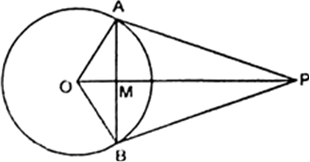
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type