Short Answer Type
Short Answer Type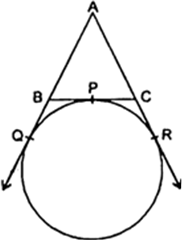
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type
Since the length of two tangents drawn from an external point are equal.
Therefore, BP = BQ
CP = CR
and AQ = AR
Perimeter of ΔABC,
= AB + BC + AC
= AB + BP + PC + AC
= (AB + BQ) + (CR + AC)
[∵ BP = BQ, CP = CR]
= AQ + AR [ ∵ AQ = AR]
= 2 AQ
It is given that : AQ = 5 cm
Therefore, perimeter (ΔABC) = 2 x 5 = 10 cm.
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer TypeFrom a point P outside a circle, with centre O tangents PA and PB are drawn as shown in the figure, prove that
(i) ⇒AOP = ∠BOP
(ii) OP is the perpendicular bisector of AB.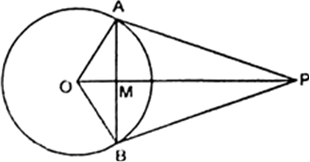
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type