267.

From a point P outside a circle, with centre O tangents PA and PB are drawn as shown in the figure, prove that

(i) ⇒AOP = ∠BOP
(ii) OP is the perpendicular bisector of AB.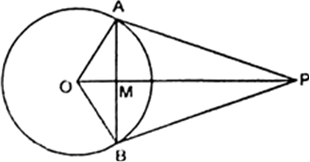

Given : Since, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ ∠OAP = ∠OBP = 90°    ..(i)
In right ΔOAP and ΔOBP,
OP = OP    (common)
OA = OB    (radii of circle)
∠OAP = ∠OBP = 90°    [from (i)]
∴ ΔOAP ≏ ΔOBP
(Using R.H.S. congruent condition)
⇒ ∠AOP = ∠BOP    [Proved]
Now, in triangles OAM and OBM,
OA = OB    (radii of circle)
∠AOM = ∠BOM [∵ ∠AOM = ∠AOP and ∠BOM = ∠BOP]
and    OM = OM    (common)
ΔOAM ≏ ΔOBM [Using SAS congruent condition]
⇒ AM = BM    ...(i)
and ∠QMA = ∠OMB
But ∠OMA + ∠OMB = 180° (linear pair) ⇒ 2∠OMA = 180° ⇒ ∠OMA = 90°
OM ⊥ AB    ...(ii)
From (i) and (ii)
⇒ OP is the perpendicular bisector of AB.