Short Answer Type
Short Answer Type
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer TypeFrom a point P outside a circle, with centre O tangents PA and PB are drawn as shown in the figure, prove that
(i) ⇒AOP = ∠BOP
(ii) OP is the perpendicular bisector of AB.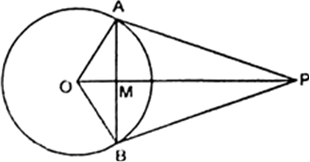
 Long Answer Type
Long Answer Type
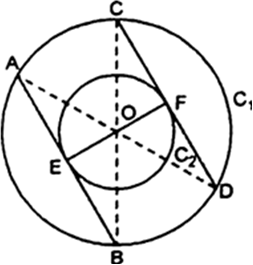
Given : Two concentric circles C1 and C2 of radii 13 cm and 8 cm respectively. AB is a diameter of the bigger circle (C1) and BD is a tangent to the smaller circle (C2).
∴ The tangent at any point of a circle is perpendicular to the radius through the point of contact.![]()
Now, in right triangle BOD, we have
OB2 = OD2 = BD2 [ Using Pythagoras theorem]![]() (13)2 = (8)2 + BD2
(13)2 = (8)2 + BD2 ![]() 169 = 64 + BD2
169 = 64 + BD2 ![]() BD2 = 169 - 64
BD2 = 169 - 64 ![]() BD2 = 105
BD2 = 105![]()
Since, perpendicular drawn from the centre to the chord bisects the chord.
(∵ ∠BEA = 90°, angle in semicircle is right angle] and, ∠OBD = ∠ABE (common)
Therefore, using AAS similar condition ΔBOD ~ ΔBAE![]()
[Proportional sides of two similar triangles]
Now, in right triangle ADE, we have
AD2 = AE2 + DE2 ![]()
= 256 + 105
= 361![]() AD = 19 cm.
AD = 19 cm.
 Short Answer Type
Short Answer Type