 Short Answer Type
Short Answer Type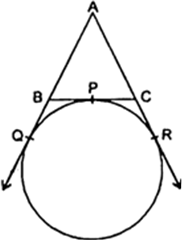
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type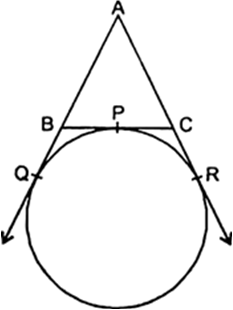
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer TypeFrom a point P outside a circle, with centre O tangents PA and PB are drawn as shown in the figure, prove that
(i) ⇒AOP = ∠BOP
(ii) OP is the perpendicular bisector of AB.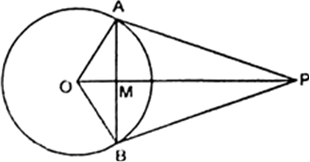
 Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type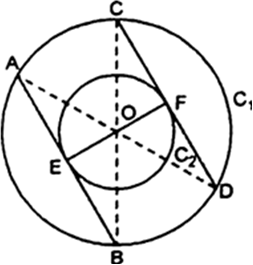

Given : XY and X‘Y’ are two parallel tangents. AB is the intercept of tangents which intersects circle at point C.
To prove : ∠AOB = 90°
Proof: ∠XAB + ∠X'BA = 180° (Consecutive interior angles)
⇒ 2∠OAB + 2∠OBA = 180°
[∵ If two tangents are drawn to a circle from an external point, then they are equally
inclined to the segment, joining the centre to that point]
⇒ ∠OAB + ∠OBA = 90°...(i)
Now, in ΔAOB
∠OAB + ∠OBA + ∠AOB = 180°
⇒ 90° + ∠AOB = 180° [Using (i)]
⇒ ∠AOB = 90°.
