Multiple Choice QuestionsIn Fig., a circle touches the side DF of EDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of EDF (in cm) is:
18
13.5
12
9
Short Answer TypeTangents PA and PB are drawn from an external point P to two concentric circle with centre O and radii 8 cm and 5 cm respectively, as shown in Fig., If AP = 15 cm, then find the length of BP.
Long Answer TypeIn fig., an isosceles triangle ABC, with AB =AB, circumscribes a circle. Prove that the point of contact P bisects the base BC.
OR
In fig., the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
Prove that the parallelogram circumscribing a circle is a rhombus.
OR
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
OR
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC.
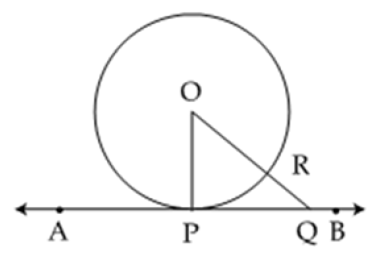
Given: AB is tangent to a circle with centre O.
To prove: OP is perpendicular to AB.
Constructions: Take a point Q on AB and join OQ.
Proof: Since Q is a point on the tangent AB, other than the point of contact P, so Q will be outside the circle.
Let OQ intersect the circle at R.
Now OQ = OR + RQ
Thus OP is shorter than any other segment among all and the shortest length is the perpendicular from O on AB.
Hence proved.
OR
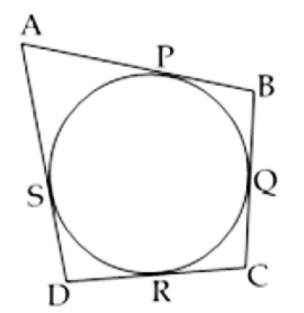
Let ABCD be a quadrilateral, circumscribing a circle.
Since the tangents drawn to the circle from an external point are equal,
we have,
AP = AS ..........(1)
BP = BQ ..........(2)
RC = QC ..........(3)
DR = DS ..........(4)
Adding, (1), (2), (3) and (4), we get
AP + PB + RC + DR = AS + BQ + QC + DS
(AP + PB ) + (RC + DR ) = (AS + DS ) + (BQ + QC)
AB + CD = AD + BC.
Switch
