Short Answer TypeIn the figure below, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to radius of the circumcircle where centre is O.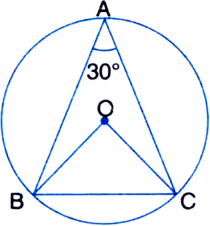
Long Answer TypeTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
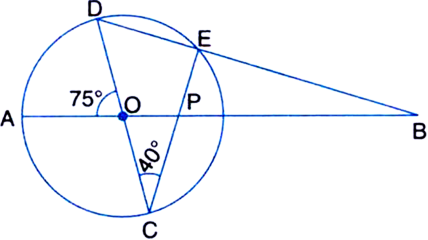
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
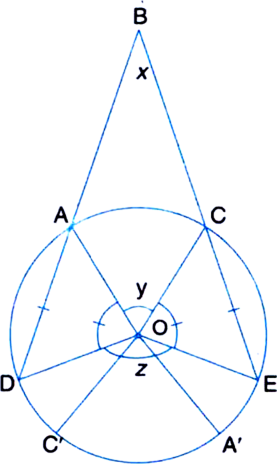
Let ∠ABC = x, ∠AOC = y and ∠DOE = z.
∠C'OD + ∠A'OE = z - y ...(1)
Let ∠C'OD = ө
Then ∠A'OE = z - y - ө
| From (1)
∠AOD = π - (∠AOC + ∠C'OD)
= π - (y + ө)
∠COE = π - (∠C'OA' + ∠A'OE)
= π - (y + z - y - ө)
= π - (z - ө)
∵ AD = CE
∴ ∠AOD = ∠COE
| Equal chords subtend equal angles at the centre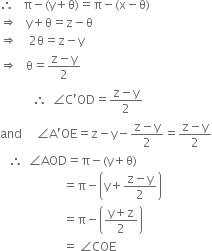
In ∆OAD,
∵ OA = OD | Radii of the same circle
∴ ∠OAD = ∠ODA
| Angles opposite to the same sides of a triangle are equal
In ∆OAD,
∠OAD + ∠ODA + ∠AOD = π
| Sum of all the angles of a triangle is π radians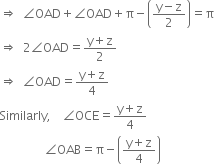
In quardrilateral AOCB
[ Sum of all the angles of a quardrilateral is 
radians ]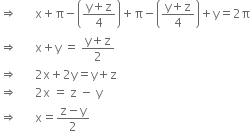
Hence, the result.
Short Answer TypeLong Answer TypeAC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
Switch
