 Long Answer Type
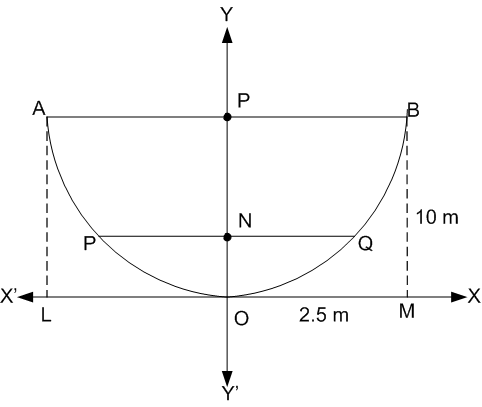
Long Answer TypeLet AB be the parabolic arch having O at the vertex and the vertical line OY as the axis.
The parabola open upwards
‚ąī ¬† Its equation is of the form¬†![]() ¬†...(i)
 ...(i)
     Width of the arch, LM = 5 m
       ![]()                     OM = 2.5 m
                    OM = 2.5 m
      Height of the arch, BM = 10 m
‚ąī Co-ordinates of point B are (2.5, 10)
Since point B lies on the parabola ![]()
‚ąī ¬† ¬†¬†![]()
‚ąī ¬† ¬† From (i), the equation of the parabola is:¬†![]()
or                       ![]()                                                            ...(ii)
                                                           ...(ii)
We have to find the width PQ of the arch at a distance ON = 2 m from the vertex.
Let                       PQ = d ![]()  NQ = 
 NQ = ![]()
‚ąī ¬† ¬†Co-ordinates of point Q are¬†![]()
Putting it in (ii), we get ![]()
Hence, the width of the arch = d = ![]()  or 2.23 (approx).
 or 2.23 (approx).
 Short Answer Type
Short Answer TypeIf a parabolic reflector is ![]()  in diameter and 20 cm deep, find the distance of its focus S from the vertex.
 in diameter and 20 cm deep, find the distance of its focus S from the vertex.
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeAn equilateral triangle is inscribed in a parabola y2 = 16x, where one vertex is at the vertex of the parabola. Find
(i) Length of each side of the triangle (ii) the area of the triangle
