Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Continuity and Differentiability

Long Answer Type

111. Find all points of discontinuity of f, where f is defined by

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell fraction numerator open vertical bar straight x close vertical bar over denominator straight x end fraction comma space space space space if space straight x not equal to 0 end cell row cell 0 comma space space space space space space space space space if space straight x equals 0 end cell end table close

136 Views

112. Find all points of discontinuity of f, where f is defined by

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell fraction numerator straight x over denominator open vertical bar straight x close vertical bar end fraction comma space if space straight x less than 0 end cell row cell space minus 1 comma space space if space straight x greater or equal than 0 end cell end table close

79 Views

113.

Find all points of discontinuity of f, where f is defined by
$straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell space straight x plus 1 comma space if space straight x greater or equal than 1 end cell row cell straight x squared plus 1 comma space if space straight x less than 1 end cell end table close$

81 Views

114.

Find all points of discontinuity of f, where f is defined by
$straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell straight x cubed minus 3 comma space if space straight x less or equal than 2 end cell row cell straight x squared plus 1 comma space if space straight x greater than 2 end cell end table close$

78 Views

115.

Find all points of discontinuity of f, where f is defined by
$straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell straight x to the power of 10 minus 1 comma space space if space straight x less or equal than 1 end cell row cell straight x squared comma space space space space space space space space space space space if space straight x greater than 1 end cell end table close$

77 Views

116. Is the function defined by

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell straight x plus 5 comma space if space straight x less or equal than 1 end cell row cell straight x minus 5 comma space if space straight x greater than 1 end cell end table close

a continuous function?

125 Views

117. Discuss the continuity of the function f, where/is defined by

straight f left parenthesis straight x right parenthesis equals open curly brackets table row cell 3 comma space space if space 0 less or equal than straight x less or equal than 1 space space end cell row cell 4 comma space space if space 1 less than straight x less than 3 end cell row cell 5 comma space if space 3 less or equal than straight x less or equal than 1 space end cell end table close

81 Views

Short Answer Type

118. Discuss the continuity of the function f, where f is defined by

straight f left parenthesis straight x right parenthesis equals open curly brackets table row cell 2 straight x comma end cell row cell 0 comma end cell row cell 4 straight x comma end cell end table close table row cell if space straight x less than 0 space space space space space space end cell row cell if space 0 less or equal than straight x less or equal than 1 end cell row cell if space straight x greater than 1 space space space space space space end cell end table

78 Views

Long Answer Type

119. Discuss the continuity of the function f , where fis defined by
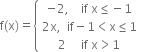
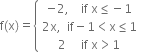
$straight f left parenthesis straight x right parenthesis equals open curly brackets table row cell negative 2 comma space space space space if space straight x less or equal than negative 1 end cell row cell 2 straight x comma space space if minus 1 less than straight x less or equal than 1 end cell row cell 2 space space space space space if space straight x greater than 1 end cell end table close$

$straight f left parenthesis straight x right parenthesis equals open curly brackets table row cell negative 2 comma space space space space if space straight x less or equal than negative 1 end cell row cell 2 straight x comma space space if minus 1 less than straight x less or equal than 1 end cell row cell 2 space space space space space if space straight x greater than 1 end cell end table close$
Function f is defined at all points of the real line.
When x < – 1, we have f(x) = – 2; which is constant and so it is continuous.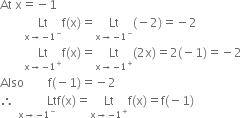
$At space straight x equals negative 1 space space space space space space space space Lt with straight x rightwards arrow negative 1 to the power of minus below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow negative 1 to the power of minus below left parenthesis negative 2 right parenthesis equals negative 2 space space space space space space space space Lt with straight x rightwards arrow negative 1 to the power of plus below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow negative 1 to the power of plus below left parenthesis 2 straight x right parenthesis equals 2 left parenthesis negative 1 right parenthesis equals negative 2 Also space space space space space space space space straight f left parenthesis negative 1 right parenthesis equals negative 2 therefore space stack space space space space space space space space space space Lt with straight x rightwards arrow negative 1 to the power of minus below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow negative 1 to the power of plus below straight f left parenthesis straight x right parenthesis equals straight f left parenthesis negative 1 right parenthesis$

∴ f is continuous at x = – 1
In the interval –1 < x < 1, we have f(x) = 2 x, which being a linear polynomial, is continuous.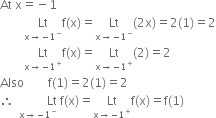
$At space straight x equals negative 1 space space space space space space space space Lt with straight x rightwards arrow negative 1 to the power of minus below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow negative 1 to the power of minus below left parenthesis 2 straight x right parenthesis equals 2 left parenthesis 1 right parenthesis equals 2 space space space space space space space space Lt with straight x rightwards arrow negative 1 to the power of plus below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow negative 1 to the power of plus below left parenthesis 2 right parenthesis equals 2 Also space space space space space space space space straight f left parenthesis 1 right parenthesis equals 2 left parenthesis 1 right parenthesis equals 2 therefore space stack space space space space space space space space space space Lt space with straight x rightwards arrow negative 1 to the power of minus below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow negative 1 to the power of plus below straight f left parenthesis straight x right parenthesis equals straight f left parenthesis 1 right parenthesis$
∴ f is continuous at x = 1
When x > 1, we have f (x) = 2. which is constant and so it is continuous.

80 Views

Short Answer Type

120. Show that the function of given by

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell straight x comma space space space space if space straight x greater or equal than 1 end cell row cell straight x squared comma space if space straight x less than 1 end cell end table close

80 Views