Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Continuity and Differentiability

Short Answer Type

141. Examine the derivability of the following function:

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell straight x minus 1 comma space space space straight x less than 2 end cell row cell 2 straight x minus 3 comma space straight x greater or equal than 2 end cell end table close at space straight x equals 2

80 Views

Long Answer Type

142. For what choices of a and b is the function

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left columnspacing 1.4ex end attributes row cell straight x squared comma end cell cell straight x less or equal than straight c end cell row cell straight a space straight x plus straight b comma end cell cell straight x greater than straight c end cell end table close differentiable space at space straight x equals straight c ?

75 Views

143. Write an example of a function which is everywhere continuous but not differentiable at exactly 3 points.

72 Views

Short Answer Type

144. Does there exist a function which is continuous everywhere but not differentiable at exactly two points ? Justify your answer.

Consider the function f given by
f(x) = |x - 1| + |x - 2|
This function is continuous everywhere
Differentiability at x = 1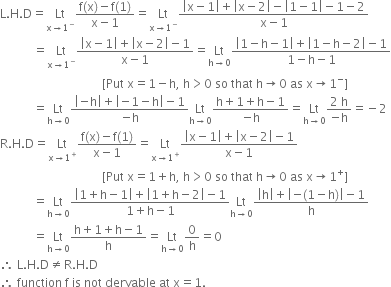
$straight L. straight H. straight D equals Lt with straight x rightwards arrow 1 to the power of minus below fraction numerator straight f left parenthesis straight x right parenthesis minus straight f left parenthesis 1 right parenthesis over denominator straight x minus 1 end fraction equals Lt with straight x rightwards arrow 1 to the power of minus below fraction numerator open vertical bar straight x minus 1 close vertical bar plus open vertical bar straight x minus 2 close vertical bar minus open vertical bar 1 minus 1 close vertical bar minus 1 minus 2 over denominator straight x minus 1 end fraction space space space space space space space space space space space equals Lt with straight x rightwards arrow 1 to the power of minus below fraction numerator open vertical bar straight x minus 1 close vertical bar plus open vertical bar straight x minus 2 close vertical bar minus 1 over denominator straight x minus 1 end fraction equals Lt with straight h rightwards arrow 0 below fraction numerator open vertical bar 1 minus straight h minus 1 close vertical bar plus open vertical bar 1 minus straight h minus 2 close vertical bar minus 1 over denominator 1 minus straight h minus 1 end fraction space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space left square bracket Put space straight x equals 1 minus straight h comma space straight h greater than 0 space so space that space straight h rightwards arrow 0 space as space straight x rightwards arrow 1 to the power of minus right square bracket space space space space space space space space space space space equals Lt with straight h rightwards arrow 0 below fraction numerator open vertical bar negative straight h close vertical bar plus open vertical bar negative 1 minus straight h close vertical bar minus 1 over denominator negative straight h end fraction Lt with straight h rightwards arrow 0 below fraction numerator straight h plus 1 plus straight h minus 1 over denominator negative straight h end fraction equals Lt with straight h rightwards arrow 0 below fraction numerator 2 space straight h over denominator negative straight h end fraction equals negative 2 straight R. straight H. straight D equals Lt with straight x rightwards arrow 1 to the power of plus below fraction numerator straight f left parenthesis straight x right parenthesis minus straight f left parenthesis 1 right parenthesis over denominator straight x minus 1 end fraction equals Lt with straight x rightwards arrow 1 to the power of plus below fraction numerator open vertical bar straight x minus 1 close vertical bar plus open vertical bar straight x minus 2 close vertical bar minus 1 over denominator straight x minus 1 end fraction space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space left square bracket Put space straight x equals 1 plus straight h comma space straight h greater than 0 space so space that space straight h rightwards arrow 0 space as space straight x rightwards arrow 1 to the power of plus right square bracket space space space space space space space space space space space equals Lt with straight h rightwards arrow 0 below fraction numerator open vertical bar 1 plus straight h minus 1 close vertical bar plus open vertical bar 1 plus straight h minus 2 close vertical bar minus 1 over denominator 1 plus straight h minus 1 end fraction Lt with straight h rightwards arrow 0 below fraction numerator open vertical bar straight h close vertical bar plus open vertical bar negative left parenthesis 1 minus straight h right parenthesis close vertical bar minus 1 over denominator straight h end fraction space space space space space space space space space space space equals Lt with straight h rightwards arrow 0 below fraction numerator straight h plus 1 plus straight h minus 1 over denominator straight h end fraction equals Lt with straight h rightwards arrow 0 below 0 over straight h equals 0 therefore space straight L. straight H. straight D not equal to straight R. straight H. straight D therefore space function space straight f space is space not space dervable space at space straight x equals 1.$
Similarly f is not derivable at x = 2. Also f is differentiable at any other point.
Hence the result.