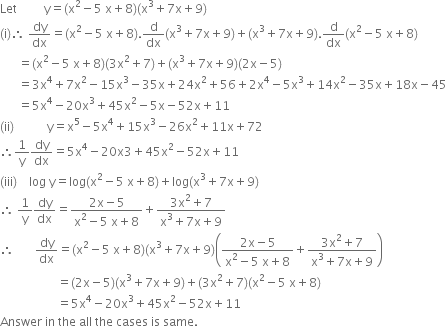Short Answer Type
Short Answer TypeDifferentiate (x2-5x+8)(x3+7x+ 9) in three ways mentioned below :
(i) by using product rule.
(ii) by expanding the product to obtain a single polynomial.
(iii) by logarithmic differentiation.
Also verify that three answers so obtained are the same.