590.

Verify Rolle's Theorem for the function f(x) = x (x²-4) in the interval [-2, 2].

 Here f(x) = x (x²-4) = x³-4 x
It is a polynomial in x
(i) Since every polynomial in x is a continuous function for every value of x
∴ f(x) is continuous in [-2, 2]
(ii) f'(x) = 3 x²-4, which exists in (-2, 2)
∴ f(x) is derivable in (-2, 2)
(iii) f(-2) = 0, f(2) = 0
∴ f(-2) = f(2)
∴ f(x) satisfies all the conditions of Rolle's Theorem.
∴ there must exist at least one real value of c such that f'(c) = 0 where - 2 < c < 2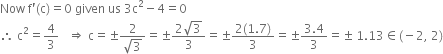

∴ Rolle's Theorem is verified.