 Short Answer Type
Short Answer TypeFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).
If A and B are (– 2, – 2) and (2, – 4), respectively, find the coordinates of P such that ![]() and P lies on the line segment Ab.
and P lies on the line segment Ab.
 Long Answer Type
Long Answer TypeFind the coordinates of the points which divide the line segment joining A(– 2, 2) and B(2, 8) into four equal parts.
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (– 1, 4) and (– 2, – 1) taken in order.
 Short Answer Type
Short Answer TypeFind the area of the triangle whose vertices are:
(–5, –1), (3, –5), (5, 2)
Let the given points be A(-5, -1), B(3, -5) and C(5, 2).
Here, we have
x1 = -5, y1 = -1
x2 = 3, y2 = -5
and x3 = 5, y3 = 2
Now, Area of ∆ABC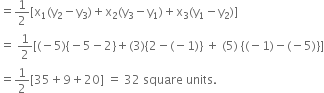
In each of the following find the value of ‘k’, for which the points are collinear
(7, –2), (5, 1), (3, k)
In each of the following find the value of ‘k’, for which the points are collinear
(8, 1), (k, – 4), (2, –5)
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
 Long Answer Type
Long Answer TypeFind the area of the quadrilateral whose vertices, taken in order, are (– 4, – 2), (– 3, – 5), (3, – 2) and (2, 3).
