 Short Answer Type
Short Answer TypeIn Figure, the vertices of Δ ABC are A(4, 6), B(1, 5) and C(7, 2). A line segment DE is drawn to intersect the sides AB and AC at D and E respectively such that ![]()
Calculate the area of Δ ADE and compare it with an area of Δ ABC.
The points A (4, 7), B (p, 3) and C (7, 3) are the vertices a right triangle, right-angled at B find the value of p.
Find the relation between x and y if the points A (x, y), B (-5, 7) and C (-4, 5) are collinear.
If the coordinates of points A and B are (-2, -2) and (2, -4) respectively, find the coordinates of P such that AP = 3/7 AB, where P lies on the line segment AB.
 Long Answer Type
Long Answer TypeFind the values of k so that the area of the triangle with vertices (1,-1), (-4, 2k) and (-k, 5) is 24 sq. units
 Short Answer Type
Short Answer TypeIf the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k?
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (7/2, y), find the value of y.
Let A(x1, y1)=A(2, 1), B(x2, y2)=B(3,−2) and C(x3, y3)=C(7/2,y).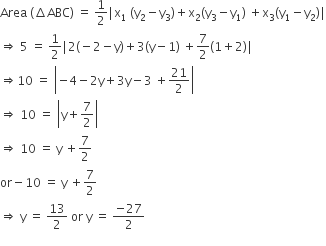
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type