 Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeSolve:![]()
The given equation is
![]()
or ![]()
or ![]()
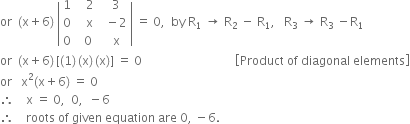
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeLet the three digit numbers A28,3B9 and 62C where A, B, and C are any integers between 0 and 9, be divisible by a fixed integer k. Show that the determinant
is divisible by k.
 Long Answer Type
Long Answer Type Multiple Choice Questions
Multiple Choice QuestionsLet A be a square matrix of order 3 × 3, then | kA | is equal to
