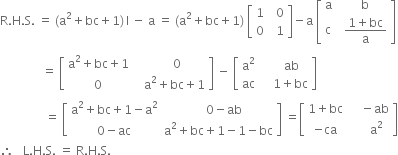Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

If $straight A space equals open square brackets table row 2 cell space space space minus 3 end cell row 3 cell space space space space space space 4 end cell end table close square brackets comma space$ show that $straight A squared minus 6 straight A plus 17 space straight I space equals space straight O.$ Hence find $straight A to the power of negative 1 end exponent.$

84 Views

182.

For the matrix $straight A space equals space open square brackets table row 2 cell space space space minus 1 end cell row 3 cell space space space space space space 2 end cell end table close square brackets comma$ show that A² – 4 A + 7 I = O. Hence obtain A^–1.

73 Views

Long Answer Type

183.

Show that the matrix $straight A space equals space open square brackets table row 2 cell space space space space space 3 end cell row 1 cell space space space space 2 end cell end table close square brackets$ satisfies the equation A² – 4A + I = O and hence find A^–1.

71 Views

184.

If $straight A space equals space open square brackets table row cell space space 3 end cell cell space space space space 1 end cell row cell negative 1 end cell cell space space space space 2 end cell end table close square brackets comma$ show that A² – 5A + 7 I = O. Hence find A ^–1.

72 Views

185.

For the matrix $straight A space equals space open square brackets table row 3 cell space space space 2 end cell row 1 cell space space space 1 end cell end table close square brackets comma$ find the numbers a and b such that A² + aA + bI = O. Hence find A^–1.

69 Views

Short Answer Type

186. If A is square matrix such that A³ = I, prove that A is non-singular and find adj. A and prove that A^–1 = A².

94 Views

187. For the matrix

straight A space equals space open square brackets table row 3 cell space space space space space space 1 end cell row 7 cell space space space space space 5 end cell end table close square brackets comma

find x and y so that A² + xI = yA. Hence find A^–1 .

126 Views

Long Answer Type

188.

If $straight A space equals space open square brackets table row 1 cell space space space space space tanx end cell row cell negative tanx end cell cell space space space 1 end cell end table close square brackets comma space space space space then space straight A apostrophe straight A to the power of negative 1 end exponent space equals space open square brackets table row cell cos space 2 straight x end cell cell space space space space space minus sin space 2 straight x end cell row cell sin space 2 straight x end cell cell space space space space space space space space cos space 2 straight x end cell end table close square brackets$

79 Views

189.
Find the inverse of the matrix $straight A space equals space open square brackets table row straight a cell space space straight b end cell row straight c cell space space fraction numerator 1 plus bc over denominator straight a end fraction end cell end table close square brackets$ and show that a A ^-1 = (a² + b c + 1) I – a A.

Here $straight A space equals open square brackets table row straight a cell space space space space straight b end cell row straight c cell space space space space space fraction numerator 1 plus bc over denominator straight a end fraction end cell end table close square brackets$

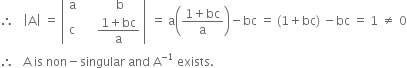
$therefore space space space open vertical bar straight A close vertical bar space equals space open vertical bar table row straight a cell space space space space space space straight b end cell row straight c cell space space space space space fraction numerator 1 plus bc over denominator straight a end fraction end cell end table close vertical bar space equals space straight a open parentheses fraction numerator 1 plus bc over denominator straight a end fraction close parentheses minus bc space equals space left parenthesis 1 plus bc right parenthesis space minus bc space equals space 1 space not equal to space 0 therefore space space space straight A space is space non minus singular space and space straight A to the power of negative 1 end exponent space exists. space$
Co-factors of the elements of the first row of | A | are $fraction numerator 1 plus bc over denominator straight a end fraction comma space$ -c respectively.
Co-factors of the elements of the second row of | A | are b , a respectively.
$therefore space space space space space adj. space straight A space equals space open square brackets table row cell fraction numerator 1 plus bc over denominator straight a end fraction end cell cell space space space minus straight c end cell row cell negative straight b end cell cell space space space space straight a end cell end table close square brackets space space equals space open square brackets table row cell fraction numerator 1 plus bc over denominator straight a end fraction end cell cell space space space minus straight b end cell row cell negative straight c end cell cell space space space space straight a end cell end table close square brackets$

Now, $straight A to the power of negative 1 end exponent space equals space fraction numerator adj. space straight A over denominator open vertical bar straight A close vertical bar end fraction space equals space open square brackets table row cell fraction numerator 1 plus bc over denominator straight a end fraction end cell cell negative straight b end cell row cell negative straight c end cell straight a end table close square brackets comma space space as space space open vertical bar straight A close vertical bar space equals space 1$

$straight L. straight H. straight S. space equals space aA to the power of negative 1 end exponent space equals space straight a open square brackets table row cell fraction numerator 1 plus bc over denominator straight a end fraction end cell cell space space space minus straight b end cell row cell negative straight c end cell cell space space space space space space straight a end cell end table close square brackets space equals space open square brackets table row cell 1 plus bc end cell cell space space space minus ab end cell row cell negative ca end cell cell space space space space space space straight a squared end cell end table close square brackets$

$straight R. straight H. straight S. space equals space left parenthesis straight a squared plus bc plus 1 right parenthesis thin space straight I space minus space straight a space equals space left parenthesis straight a squared plus bc plus 1 right parenthesis space open square brackets table row 1 cell space space 0 end cell row 0 cell space space 1 end cell end table close square brackets minus straight a space open square brackets table row straight a cell space space straight b end cell row straight c cell space space fraction numerator 1 plus bc over denominator straight a end fraction end cell end table close square brackets space space space space space space space space space space space space space space equals space open square brackets table row cell straight a squared plus bc plus 1 end cell cell space space space space space 0 end cell row 0 cell space space space straight a squared plus bc plus 1 end cell end table close square brackets space minus space open square brackets table row cell straight a squared end cell cell space space space space space ab end cell row ac cell space space space space 1 plus bc end cell end table close square brackets space space space space space space space space space space space space space space space equals space open square brackets table row cell straight a squared plus bc plus 1 minus straight a squared end cell cell space space space space 0 minus ab end cell row cell 0 minus ac end cell cell straight a squared plus bc plus 1 minus 1 minus bc end cell end table close square brackets space equals open square brackets table row cell 1 plus bc end cell cell space space space space minus ab end cell row cell negative ca end cell cell space space space space space straight a squared end cell end table close square brackets therefore space space space straight L. straight H. straight S. space equals space straight R. straight H. straight S.$

75 Views

190.

If $straight A space equals space open square brackets table row 1 cell space space space space 3 end cell row 2 cell space space space space 7 end cell end table close square brackets space space and space straight B space equals space open square brackets table row 3 cell space space space space 4 end cell row 6 cell space space space space 2 end cell end table close square brackets comma$
verify (AB)^–1 = B ^–1 A^–1