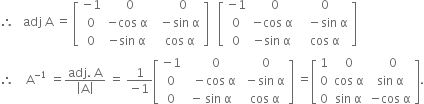Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Find $straight A to the power of negative 1 end exponent$ if $straight A space equals space open square brackets table row 0 cell space space space space 1 end cell cell space space space space 1 end cell row 1 cell space space space space 0 end cell cell space space space 1 end cell row 1 cell space space space space 1 end cell cell space space space 0 end cell end table close square brackets$ Also show that $straight A to the power of negative 1 end exponent space space equals fraction numerator straight A squared minus 3 straight I over denominator 2 end fraction.$

77 Views

202.

If $straight A space equals space open square brackets table row 1 cell space space 3 end cell cell space space space 3 end cell row 1 cell space space 4 end cell cell space space 3 end cell row 1 cell space 3 end cell cell space space space 4 end cell end table close square brackets comma$ then verify that A adj A = | A | I. Also find A .

86 Views

Short Answer Type

203.

Find the inverse of the matrix $open square brackets table row 1 cell space space 2 end cell cell space space 3 end cell row 0 cell space space 2 end cell cell space space 4 end cell row 0 cell space space 0 end cell cell space space 5 end cell end table close square brackets$ .

76 Views

Long Answer Type

204.

Find the inverse of the matrix $open square brackets table row 1 cell space space space space 0 end cell cell space space space space 0 end cell row 3 cell space space space 3 end cell cell space space space space space 0 end cell row 5 cell space space space space 2 end cell cell space space minus 1 end cell end table close square brackets$

73 Views

205.

Find the inverse of the matrix:
$open square brackets table row 2 cell space space space space space 1 end cell cell space space space space space 3 end cell row 4 cell space minus 1 end cell cell space space space space space 0 end cell row cell negative 7 end cell cell space space space space space 2 end cell cell space space space space 1 end cell end table close square brackets$

74 Views

206.

Find the inverse of the matrix:
$open square brackets table row cell space space space 2 end cell cell space space space space minus 1 end cell cell space space space space space 1 end cell row cell negative 1 end cell cell space space space space space space space 2 end cell cell space space minus 1 end cell row cell space space 1 end cell cell space space space space minus 1 end cell cell space space space space space 2 end cell end table close square brackets$

75 Views

Short Answer Type

207.

Find the inverse of the matrix:
$open square brackets table row 2 cell space space minus 3 end cell cell space space space space 3 end cell row 3 cell space space space space space 2 end cell cell space space space space space 3 end cell row 3 cell space space minus 2 end cell cell space space space space 2 end cell end table close square brackets$

72 Views

Long Answer Type

208.

Find the inverse of the matrix:
$open square brackets table row 1 cell space space 2 end cell cell space space 2 end cell row 2 cell space 1 end cell cell space 2 end cell row 2 cell space 2 end cell cell space 1 end cell end table close square brackets$

82 Views

209.
Find the inverse of the matrix:
$open square brackets table row 1 cell space 0 end cell cell space 0 end cell row 0 cell space space cos space straight alpha end cell cell space space sin space straight alpha end cell row 0 cell space sin space straight alpha end cell cell space space minus cos space straight alpha end cell end table close square brackets$

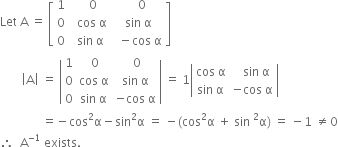
Let space straight A space equals space open square brackets table row 1 cell space space space 0 end cell cell space space space 0 end cell row 0 cell space space cos space straight alpha end cell cell space sin space straight alpha end cell row 0 cell space sin space straight alpha end cell cell space space minus cos space straight alpha end cell end table close square brackets space space space space space space space open vertical bar straight A close vertical bar space equals space open vertical bar table row 1 cell space 0 end cell cell space 0 end cell row 0 cell cos space straight alpha end cell cell sin space straight alpha end cell row 0 cell sin space straight alpha end cell cell negative cos space straight alpha end cell end table close vertical bar space equals space 1 open vertical bar table row cell cos space straight alpha end cell cell space space space sin space straight alpha end cell row cell sin space straight alpha end cell cell negative cos space straight alpha end cell end table close vertical bar space space space space space space space space space space space space space space equals negative cos squared straight alpha minus sin squared straight alpha space equals space minus left parenthesis cos squared straight alpha space plus space sin space squared straight alpha right parenthesis space equals space minus 1 space not equal to 0 therefore space space straight A to the power of negative 1 end exponent space exists.

Co-factors of the elements of first row of | A | are

open vertical bar table row cell cos space straight alpha end cell cell space space space sin space straight alpha end cell row cell sin space straight alpha end cell cell negative cos space straight alpha end cell end table close vertical bar comma space space space minus open vertical bar table row 0 cell space space space sin space straight alpha end cell row 0 cell negative cos space straight alpha end cell end table close vertical bar comma space space open vertical bar table row 0 cell space space space space space cos space straight alpha end cell row 0 cell space space space minus space sin space straight alpha end cell end table close vertical bar

i.e. α cos² α sin² α 0 , 0 i.e. – 1, 0, 0 respectively.
Co-factors of the elements of second row of | A | are
$negative open vertical bar table row 0 cell space space space space 0 end cell row cell sin space straight alpha end cell cell space space space minus cos space straight alpha end cell end table close vertical bar comma space space space open vertical bar table row 1 cell space space space space space space space 0 end cell row 0 cell space space space minus cos space straight alpha end cell end table close vertical bar comma space space space minus open vertical bar table row 1 cell space space space 0 end cell row 0 cell space space space sin space straight alpha end cell end table close vertical bar$

i.e. 0, cos α, – sin α, respectively.
Co-factors of the elements of third row of | A | are
$open vertical bar table row 0 cell space space space 0 end cell row cell cos space space straight alpha end cell cell space space sin space straight alpha end cell end table close vertical bar comma space space minus open vertical bar table row 1 cell space space 0 end cell row 0 cell space space sin space straight alpha end cell end table close vertical bar comma space space open vertical bar table row 1 cell space space space 0 end cell row 0 cell space space space space cos space straight alpha end cell end table close vertical bar$
i.e. 0, – sin α, cos α respectively.

$therefore space space space adj space straight A space equals space open square brackets table row cell negative 1 end cell cell space space 0 end cell cell space space space space 0 end cell row 0 cell negative cos space straight alpha end cell cell space space minus sin space straight alpha end cell row 0 cell negative sin space straight alpha end cell cell space space cos space straight alpha end cell end table close square brackets space space space open square brackets table row cell negative 1 end cell cell space space 0 end cell cell space 0 end cell row 0 cell negative cos space straight alpha end cell cell space space space minus sin space straight alpha end cell row 0 cell negative sin space straight alpha end cell cell space cos space straight alpha end cell end table close square brackets therefore space space space space straight A to the power of negative 1 end exponent space equals fraction numerator adj. space straight A over denominator open vertical bar straight A close vertical bar end fraction space equals space fraction numerator 1 over denominator negative 1 end fraction open square brackets table row cell negative 1 end cell cell space space space 0 end cell cell space space 0 end cell row 0 cell space space minus cos space straight alpha end cell cell space minus sin space straight alpha end cell row 0 cell negative space sin space straight alpha end cell cell space cos space straight alpha end cell end table close square brackets space equals open square brackets table row 1 0 cell space space 0 end cell row 0 cell cos space straight alpha end cell cell sin space straight alpha end cell row 0 cell sin space straight alpha end cell cell negative cos space straight alpha end cell end table close square brackets.$

74 Views

210.

If $straight A space equals space open square brackets table row 1 cell space 2 end cell cell space space 5 end cell row 2 cell space 3 end cell cell space 1 end cell row cell negative 1 end cell cell space 1 end cell cell space 1 end cell end table close square brackets comma$ then compute the inverse of A and verify that A^–1 A = I = A A^–1

75 Views

Previous Year Papers

Test Series

Test Yourself

Long Answer Type

Short Answer Type

Long Answer Type

Short Answer Type

Long Answer Type

209. Find the inverse of the matrix: