Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Determinants

Long Answer Type

251.

Using matrices, solve the following system of equations:
2x + y – 3r = 13
x + y – z = 6
2x – y + 4z = – 12

74 Views

252.

Using matrices, solve the following system of linear equations.
3x + 4y + 2z = 8
2y –3z = 3
x – 2y + 6z = –2

87 Views

253. Using matrices, solve the following system of linear equations:
x – y + z = 1
2x – yz = 2
x – 2y – z

81 Views

254.

Using matrices, solve the following system of linear equations:
x – y = 3
2x + 3y + 4z = 17
y + 2 z = 7

75 Views

255.
Solve by matrix method:
y + 2z = – 8
x + 2y + 3z = – 14
3x + y + z = – 8

The given equations are
y + 2z = – 8
x + 2y + 3z = – 14
3x + y + z = – 8
These equations can be written as
   $open square brackets table row 0 cell space space 1 end cell cell space space 2 end cell row 1 cell space space 2 end cell cell space 3 end cell row 3 cell space 1 end cell cell space 1 end cell end table close square brackets space equals space open square brackets table row straight x row straight y row straight z end table close square brackets space equals space open square brackets table row cell negative 8 end cell row cell negative 14 end cell row cell negative 8 end cell end table close square brackets$

or    $AX space equals space straight B space where space straight A space equals space open square brackets table row 0 cell space space 1 end cell cell space space 2 end cell row 1 cell space space 2 end cell cell space space 3 end cell row 3 cell space space 1 end cell cell space space 1 end cell end table close square brackets comma space space space straight X space equals space open square brackets table row straight x row straight y row straight z end table close square brackets comma space space straight B space equals space open square brackets table row cell negative 8 end cell row cell negative 14 end cell row cell negative 8 end cell end table close square brackets space space$
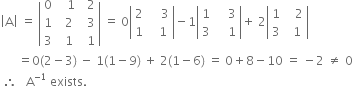
$open vertical bar straight A close vertical bar space equals space open vertical bar table row 0 cell space space space 1 end cell cell space space 2 end cell row 1 cell space space 2 end cell cell space space 3 end cell row 3 cell space space 1 end cell cell space space 1 end cell end table close vertical bar space equals space 0 open vertical bar table row 2 cell space space space space 3 end cell row 1 cell space space space 1 end cell end table close vertical bar minus 1 open vertical bar table row 1 cell space space space space 3 end cell row 3 cell space space space space 1 end cell end table close vertical bar plus space 2 open vertical bar table row 1 cell space space space 2 end cell row 3 cell space space 1 end cell end table close vertical bar space space space space space space equals 0 left parenthesis 2 minus 3 right parenthesis space minus space 1 left parenthesis 1 minus 9 right parenthesis space plus space 2 left parenthesis 1 minus 6 right parenthesis space equals space 0 plus 8 minus 10 space equals space minus 2 space not equal to space 0 space therefore space space space straight A to the power of negative 1 end exponent space exists.$
Co-factors of the elements of first row of | A | are
$open vertical bar table row 2 cell space space space 3 end cell row 1 cell space space 1 end cell end table close vertical bar comma space space space minus open vertical bar table row 1 cell space space space 3 end cell row 3 cell space space space 1 end cell end table close vertical bar comma space space space space open vertical bar table row 1 cell space space space space 2 end cell row 3 cell space space space 1 end cell end table close vertical bar$
i.e. –1, 8, –5 respectively.
Co-factors of the elements of second row of | A | are
$negative open vertical bar table row 1 cell space space space 2 end cell row 1 cell space space 1 end cell end table close vertical bar comma space space space space open vertical bar table row 0 cell space space 2 end cell row 3 cell space space 1 end cell end table close vertical bar comma space space space minus open vertical bar table row 0 cell space space space 1 end cell row 3 cell space space 1 end cell end table close vertical bar$
i.e. 1, –6, 3 respectively.
Co-factors of the elements of third row of | A | are
$open vertical bar table row 1 cell space space space 2 end cell row 2 cell space space space 3 end cell end table close vertical bar comma space space space space minus open vertical bar table row 0 cell space space space space 2 end cell row 1 cell space space space 3 end cell end table close vertical bar comma space space open vertical bar table row 0 cell space space space 1 end cell row 1 cell space space 2 end cell end table close vertical bar$
i.e.   –1, 2, –1 respectively.
$therefore space space space space adj. space straight A space equals space open square brackets table row cell negative 1 end cell cell space space space space 8 end cell cell space space minus 5 end cell row cell space space 1 end cell cell space space minus 6 end cell cell space space space space space space 3 end cell row cell negative 1 end cell cell space space space space space 2 end cell cell space space minus 1 end cell end table close square brackets to the power of apostrophe space equals space open square brackets table row cell negative 1 end cell cell space space space space space 1 end cell cell space space space minus 1 end cell row cell space space space space 8 end cell cell space space minus 6 end cell cell space space space space space space space 2 end cell row cell space space minus 5 end cell cell space space space space space 3 end cell cell space space minus 1 end cell end table close square brackets therefore space space space space straight A to the power of negative 1 end exponent equals space fraction numerator adj space straight A over denominator open vertical bar straight A close vertical bar end fraction space equals space minus 1 half open square brackets table row cell negative 1 end cell cell space space space space space 1 end cell cell space space space minus 1 end cell row cell space space space 8 end cell cell space space minus 6 end cell cell space space space space space space 2 end cell row cell negative 5 end cell cell space space space space 3 end cell cell space space minus 1 end cell end table close square brackets Now space AX space equals space straight B space space space space rightwards double arrow space space space space space space space space space space space straight X space equals space straight A to the power of negative 1 end exponent straight B therefore space space space space space space space open square brackets table row straight x row straight y row straight z end table close square brackets space equals space minus 1 half open square brackets table row cell negative 1 end cell cell space space space space space 1 end cell cell space space space minus 1 end cell row cell space space space space 8 end cell cell space space minus 6 end cell cell space space space space space space 2 end cell row cell space minus 5 end cell cell space space space space 3 end cell cell space space minus 1 end cell end table close square brackets space open square brackets table row cell negative 8 end cell row cell negative 14 end cell row cell negative 8 end cell end table close square brackets rightwards double arrow space space space space space open square brackets table row straight x row straight y row straight z end table close square brackets space equals space minus 1 half open square brackets table row cell 8 minus 14 plus 8 end cell row cell negative 64 plus 84 minus 16 end cell row cell 40 minus 42 plus 8 end cell end table close square brackets rightwards double arrow space space space space space open square brackets table row straight x row straight y row straight z end table close square brackets space equals space minus 1 half open square brackets table row 2 row 4 row 6 end table close square brackets space space space space space space space space space space space space space space space space space space space space space space space space rightwards double arrow space space space space space open square brackets table row straight x row straight y row straight z end table close square brackets space equals space open square brackets table row cell negative 1 end cell row cell negative 2 end cell row cell negative 3 end cell end table close square brackets therefore space space space space straight x space equals space minus 1 comma space space space space space space straight y space equals space minus 2 comma space space space space space straight z space equals space minus 3 space is space required space solution.$

73 Views

256.

Solve the following system of equations by matrix method:
3x – 2y + 3z = 8
2x + y – z = 1
4x – 3y + 2z = 4

89 Views

257.

Solve the following equation by matrix method:
$2 straight x plus straight y plus straight z space equals space 1 straight x minus 2 straight y minus straight z space equals 3 over 2 space space 3 straight y minus 5 straight z space space equals 9$