If   find A-1, Using A-1, solve the following system of lin
    • Zigya Logo

    Previous Year Papers

    Download Solved Question Papers Free for Offline Practice and view Solutions Online.

    Test Series

    Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

    Test Yourself

    Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.
    Advertisement

    Determinants

    Multiple Choice QuestionsLong Answer Type

    301.

    Solve by matrix method:
    3 over straight x plus 4 over straight y plus 7 over straight z space equals space 14 2 over straight x minus 1 over straight y plus 3 over straight z space equals space 4 1 over straight x plus 2 over straight y minus 3 over straight z space equals space 0

    92 Views
    Answer
    302.

    Solve  the system of the following equations:
    2 over straight x plus 3 over straight y plus 10 over straight z space equals space 4 4 over straight x minus 6 over straight y plus 5 over straight z space equals space 1 6 over straight x plus 9 over straight y minus 20 over straight z space equals space 2

    75 Views
    Answer
    Advertisement
    Zigya App

    303.

    If straight A space equals space open square brackets table row 2 cell space space space minus 3 end cell cell space space space space 5 end cell row 3 cell space space space space space 2 end cell cell space minus 4 end cell row 1 cell space space space 1 end cell cell space minus 2 end cell end table close square brackets comma  find A-1, Using A-1, solve the following system of linear equations.
    2x – 3y + 5z = 16
    3x + 2y – 4z = – 4
    x + y – 2z = – 3

    Here,
          straight A space equals space open square brackets table row 2 cell space space space minus 3 end cell cell space space space 5 end cell row 3 cell space space space space space 2 end cell cell negative 4 end cell row 1 cell space space space 1 end cell cell negative 2 end cell end table close square brackets

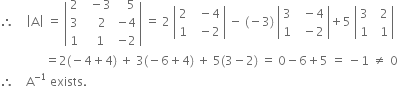
    therefore space space space space open vertical bar straight A close vertical bar space equals space open vertical bar table row 2 cell space space minus 3 end cell cell space space space 5 end cell row 3 cell space space space 2 end cell cell negative 4 end cell row 1 cell space space 1 end cell cell negative 2 end cell end table close vertical bar space equals space 2 space open vertical bar table row 2 cell space space minus 4 end cell row 1 cell space space minus 2 end cell end table close vertical bar space minus space left parenthesis negative 3 right parenthesis space open vertical bar table row 3 cell space space minus 4 end cell row 1 cell space space minus 2 end cell end table close vertical bar plus 5 space open vertical bar table row 3 cell space space 2 end cell row 1 cell space space 1 end cell end table close vertical bar space space space space space space space space space space space space space space space equals 2 left parenthesis negative 4 plus 4 right parenthesis space plus space 3 left parenthesis negative 6 plus 4 right parenthesis space plus space 5 left parenthesis 3 minus 2 right parenthesis space equals space 0 minus 6 plus 5 space equals space minus 1 space not equal to space 0 therefore space space space space straight A to the power of negative 1 end exponent space exists.
    Co-factors of the elements of first row of | A | are
    open vertical bar table row 2 cell space space space minus 4 end cell row 1 cell space space minus 2 end cell end table close vertical bar comma space space space space minus open vertical bar table row 3 cell space space space minus 4 end cell row 1 cell space space minus 2 end cell end table close vertical bar comma space space space space open vertical bar table row 3 cell space space space 2 end cell row 1 cell space space 1 end cell end table close vertical bar
    i.e. 0, 2, 1 respectively
    Co-factors of the elements of second row of | A | are
    negative open vertical bar table row cell negative 3 end cell cell space space space space 5 end cell row 1 cell space minus 2 end cell end table close vertical bar comma space space space open vertical bar table row 2 cell space space space space space 5 end cell row 1 cell space space minus 2 end cell end table close vertical bar comma space space space space minus open vertical bar table row 2 cell space space space minus 3 end cell row 1 cell space space space space space space 1 end cell end table close vertical bar
    i.e., –1, –9 , –5 respectively.
    Co-factors of the elements of third row of | A | are
    open vertical bar table row cell negative 3 end cell cell space space space space space space 5 end cell row 2 cell space space minus 4 end cell end table close vertical bar comma space space space space minus open vertical bar table row 2 cell space space space space space space 5 end cell row 3 cell space space space minus 4 end cell end table close vertical bar comma space space space open vertical bar table row 2 cell space space minus 3 end cell row 3 cell space space space space 2 end cell end table close vertical bar
    i.e., 2, 23, 13 respectively.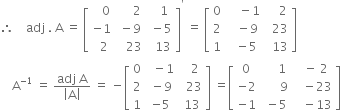
    therefore space space space space adj space. space straight A space equals space open square brackets table row cell space space space 0 end cell cell space space space space space 2 end cell cell space space space 1 end cell row cell negative 1 end cell cell space minus 9 end cell cell space minus 5 end cell row cell space space 2 end cell cell space space space 23 end cell cell space space 13 end cell end table close square brackets to the power of apostrophe space equals space open square brackets table row 0 cell space space space space minus 1 end cell cell space space space space 2 end cell row 2 cell space space space minus 9 end cell cell space space 23 end cell row 1 cell space space minus 5 end cell cell space space 13 end cell end table close square brackets space space space space straight A to the power of negative 1 end exponent space equals space fraction numerator adj space straight A over denominator open vertical bar straight A close vertical bar end fraction space equals space minus open square brackets table row 0 cell space space minus 1 end cell cell space space space 2 end cell row 2 cell space minus 9 end cell cell space space 23 end cell row 1 cell negative 5 end cell cell space 13 end cell end table close square brackets space equals open square brackets table row 0 cell space space space space space 1 end cell cell space space minus space 2 end cell row cell negative 2 end cell cell space space space space space space 9 end cell cell space space space minus 23 end cell row cell negative 1 end cell cell space minus 5 end cell cell space space space minus 13 end cell end table close square brackets space space space space space space space

    The given equations are
    2x – 3y + 5z = 16
    3x + 2y – 4z = – 4
    x + y – 2z = – 3
    These equations can be written as
                     space open square brackets table row 2 cell space space space minus 3 end cell cell space space space space space space 5 end cell row 3 cell space space space space space 2 end cell cell space minus 4 end cell row 1 cell space space space 1 end cell cell space space minus 2 end cell end table close square brackets space open square brackets table row straight x row straight y row straight z end table close square brackets space equals space open square brackets table row cell space 16 end cell row cell negative 4 end cell row cell negative 3 end cell end table close square brackets

    or space space space space space AX space equals space straight B space space where space straight A space equals space open square brackets table row 2 cell space minus 3 end cell cell space space space space 5 end cell row 3 cell space space space 2 end cell cell space minus 4 end cell row 1 cell space space 1 end cell cell negative 2 end cell end table close square brackets comma space space straight X space equals space open square brackets table row straight x row straight y row straight z end table close square brackets comma space space straight B space equals space open square brackets table row 16 row cell negative 4 end cell row cell negative 3 end cell end table close square brackets



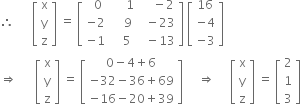
    therefore space space space space space space open square brackets table row straight x row straight y row straight z end table close square brackets space equals space open square brackets table row cell space space 0 end cell cell space space space space space 1 end cell cell space space space space minus 2 end cell row cell negative 2 end cell cell space space space space 9 end cell cell space space minus 23 end cell row cell negative 1 end cell cell space space space 5 end cell cell space space minus 13 end cell end table close square brackets space open square brackets table row 16 row cell negative 4 end cell row cell negative 3 end cell end table close square brackets rightwards double arrow space space space space space space open square brackets table row straight x row straight y row straight z end table close square brackets space equals space open square brackets table row cell 0 minus 4 plus 6 end cell row cell negative 32 minus 36 plus 69 end cell row cell negative 16 minus 20 plus 39 end cell end table close square brackets space space space space space rightwards double arrow space space space space space open square brackets table row straight x row straight y row straight z end table close square brackets space equals space open square brackets table row 2 row 1 row 3 end table close square brackets

    therefore space space space space straight x space equals 2 comma space space space space space straight y space equals space 1 comma space space space straight z space equals space 3.

    75 Views
  • Switch Icon Switch
    • Advertisement
    304.

    If straight A space equals space open square brackets table row 2 cell space space space minus 3 end cell cell space space space space 5 end cell row 3 cell space space space space 2 end cell cell negative 4 end cell row 1 cell space space space 1 end cell cell negative 2 end cell end table close square brackets comma find A –1 .
    Using A–1, solve the following system of linear equations.
    2x – 3y + 5z = 11
    3x + 2y – 4z = – 5
    x + y – 2z = – 3

    74 Views
    Answer
    Advertisement
    305.

    Compute A–1 for the following matrix 
    straight A space equals space open square brackets table row cell negative 1 end cell cell space space space space space 2 end cell cell space space space space 5 end cell row cell space space 2 end cell cell space space minus 3 end cell cell space space space 1 end cell row cell negative 1 end cell cell space space 1 end cell cell space space space space 1 end cell end table close square brackets.
    Hence solve the system of equations.
    – x + 2y+ 5 z = 2
    2x – 3y + Z = 15
    – x + y + z = – 3

    78 Views
    Answer
    306.

    Compute A–1 for the following matrix
    straight A space equals space open square brackets table row 1 cell space space space space space 2 end cell cell space space space 5 end cell row 1 cell space minus 1 end cell cell space minus 1 end cell row 2 cell space space space 3 end cell cell space minus 2 end cell end table close square brackets.
    Hence,  solve the system of equations:
    x + 2y + 5z = 10
    x – y – z = – 2
    2x + 3y – 2z = – 1

    97 Views
    Answer
    307.

    If straight A equals space open square brackets table row 3 cell space space space minus 2 end cell cell space space space space space 1 end cell row 2 cell space space space space 1 end cell cell space minus 3 end cell row cell negative 1 end cell cell space space space 2 end cell cell space space space 1 end cell end table close square brackets comma  Find A–1.

    Using A solve the following systems of linear equations:
    3x – 2y + z = 2
    2y + y – 3z = – 5
    – x + 2y + z = 6.

    75 Views
    Answer

    Multiple Choice QuestionsShort Answer Type

    308.

    Investigate for what values of a and b the simultaneous equations:
    x + y + z = 6
    x + 2y + 3z = 10
    x + 2y + az = b have a unique solution.

    86 Views
    Answer
    Advertisement

    Multiple Choice QuestionsLong Answer Type

    309.

    The sum of three numbers is 6. If we multiply third number by 3 and add second number to it, we get 11. By adding first and third numbers, we get double of the second number. Represent it algebraically and find the numbers using matrix method.

    86 Views
    Answer
    310. The cost of 4 kg. onion, 3 kg. wheat and 2 kg. rice is Rs. 60. The cost of 2 kg. onion, 4 kg. wheat and 6 kg. rice is Rs. 90. The cost of 6 kg. onion. 2 kg. wheat and 3 kg. rice is Rs. 70. Find cost of each item per kg. by matrix method.
    77 Views
    Answer
    Advertisement
    Flag Popup Icon
    Flag it
    Submit
    Flag Popup Icon
    Switch to
    flexipad
    Share It Icon
    Share it
    Share It
    Share it