Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Introduction To Three Dimensional Geometry

Short Answer Type

81. Find the co-ordinates of the centroid of triangle whose vertices are A (2, 3, -1), B (1, 3, -2) and C (3, 0, 3).

124 Views

82. The centroid of a triangle ABC is at the point (1, 1, 1). If the co-ordinates of A and B are (3, -5, 7) and (-1, 7, -6) respectively, find the co-ordinates of the point C

138 Views

83. If the origin is the centroid of triangle PQR, with vertices P(2a, 2, 6), Q(- 4, 3b, - 10) and R(8, 14, 2c). Find the values of a, b and c.

139 Views

84. Without using distance formula, show that A (-1, 2, 1), B (1, -2, 5) C (4, - 7, 8) and D (2, - 3, 4) are the vertices of a parallelogram ABCD.

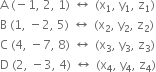
straight A space left parenthesis negative 1 comma space 2 comma space 1 right parenthesis space left right arrow space left parenthesis straight x subscript 1 comma space straight y subscript 1 comma space straight z subscript 1 right parenthesis straight B space left parenthesis 1 comma space minus 2 comma space 5 right parenthesis space left right arrow space left parenthesis straight x subscript 2 comma space straight y subscript 2 comma space straight z subscript 2 right parenthesis straight C space left parenthesis 4 comma space minus 7 comma space 8 right parenthesis space left right arrow space left parenthesis straight x subscript 3 comma space straight y subscript 3 comma space straight z subscript 3 right parenthesis straight D space left parenthesis 2 comma space minus 3 comma space 4 right parenthesis space left right arrow space left parenthesis straight x subscript 4 comma space straight y subscript 4 comma space straight z subscript 4 right parenthesis

Mid-point of diagonal AC =

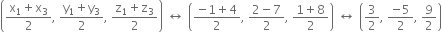
open parentheses fraction numerator straight x subscript 1 plus straight x subscript 3 over denominator 2 end fraction comma space fraction numerator straight y subscript 1 plus straight y subscript 3 over denominator 2 end fraction comma space fraction numerator straight z subscript 1 plus straight z subscript 3 over denominator 2 end fraction close parentheses space left right arrow space open parentheses fraction numerator negative 1 plus 4 over denominator 2 end fraction comma space fraction numerator 2 minus 7 over denominator 2 end fraction comma space fraction numerator 1 plus 8 over denominator 2 end fraction close parentheses space left right arrow space open parentheses 3 over 2 comma space fraction numerator negative 5 over denominator 2 end fraction comma space 9 over 2 close parentheses

...(i)

Mid- point of diagonal BD =

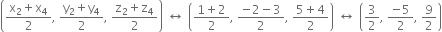
open parentheses fraction numerator straight x subscript 2 plus straight x subscript 4 over denominator 2 end fraction comma space fraction numerator straight y subscript 2 plus straight y subscript 4 over denominator 2 end fraction comma space fraction numerator straight z subscript 2 plus straight z subscript 4 over denominator 2 end fraction close parentheses space left right arrow space open parentheses fraction numerator 1 plus 2 over denominator 2 end fraction comma space fraction numerator negative 2 minus 3 over denominator 2 end fraction comma space fraction numerator 5 plus 4 over denominator 2 end fraction close parentheses space left right arrow space open parentheses 3 over 2 comma space fraction numerator negative 5 over denominator 2 end fraction comma space 9 over 2 close parentheses

...(ii)
From (i) and (ii), we observe that mid-points of AC and BD are coincident.

rightwards double arrow

Diagonals AC and BD bisect each other.
Hence, ABCD is a parllelogram.

100 Views

85. Three vertices of a parallelogram ABCD are A (3, -1, 2), B (1, 2, -4), and C (-1, 1, 2). Find the co-ordinates of the fourth vertex.

147 Views

Long Answer Type

86. The co-ordinates of the mid-points of sides BC, CA and AB of ∆ ABC are (2, 1, -1), (3, 2, 4) and (1, -2, 3) respectively. Find the co-ordinates of vertices A, B and C.

120 Views

Short Answer Type

87. Find the co-ordinates of a point P which divides the join of A (1, - 2, -1) and (1, 5, -8) internally in ratio 3 : 4.

89 Views

88. Find the co-ordinates of a point which divides the line joining points A (2, - 1, 3) and B (1, 4, 2) externally in ratio 2 : 3.

91 Views

89. Find the ratio in which the line joining points A (2, 4, - 3) and B (-3, 5, 2) is divided to XY-plane.

114 Views

90. Find the ratio in which the line joining points P (-3, 4, 5) and Q (5, 1, -1) divided by YZ-plane.

112 Views