 Long Answer Type
Long Answer TypeSolve the following problem graphically:
Minimise and Maximise Z = 3x + 9y
subject to the constraints:
x + 3y ≤ 60
x + y ≥ 10
x ≤ y
x ≥ 0, y ≥ 0
Solve the following linear programming problem graphically:
Minimise Z = 3x + 5y subject to the constraints:x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0
We are to minimise Z = x + 2y subject to the constraints 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Consider a set of rectangular cartesian axes OXY in the plane.
It is clear that any point which satisfies x ≥ 0, y ≥ 0 lies in the first quadrant.
Let us draw the graph of 2x + y = 3
For x = 0, y = 3
For y = 0, 2x = 3 or x = ![]()
![]()
Again we draw the graph of x + 2 y = 6.
For x = 0, 2 y = 6 or y = 3
For y = 0, x = 6
∴ line meets OX in B(6, 0) and OY in L(0, 3).
Since feasible region is the region which satisfies all the constraints.
∴ shaded region is the feasible region and comer points are B(6, 0), L(0, 3).
At B(6, 0), Z = 6 + 0 = 6
At L(0, 3), Z = 0 + 6 = 6
∴ 6 is the greatest value of Z at (6, 0) and (0, 3) and so on the line BL.
Since feasible region is unbounded.
∴ we are to check whether this value is maximum.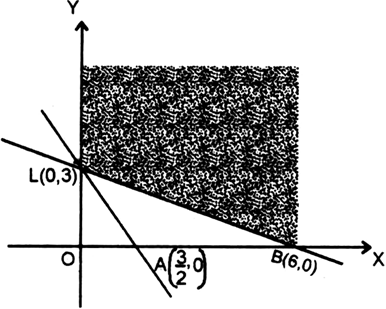
For this we draw the graph of
x + 2y < 6 ...(1)
Since (1) has no point in common with the feasible region.
∴ minimum value = 6 at all points on the line segment joining the points (6, 0) and (0, 3).
∴ minimum of Z occurs at more than two points.
