Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Linear Programming

Long Answer Type

31. A factory manufactures two type of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs. 7 and screws B at a profit of Rs. 10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit ? Determine the maximum profit.

140 Views

32. A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day. the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs 5 and that from a shade is Rs 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit?

91 Views

33. A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours tor assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should be the company manufacture in order to maximise the profit?

91 Views

34. A merchant plans to sell two types of personal computers - a desktop model and a portable model that will cost Rs. 25000 and Rs. 40000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and if his profit on the desktop model is Rs 4500 and on portable model is Rs 5000.

105 Views

35. A diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1400 units of calories. Two foods A and B are available at a cost of Rs. 5 and Rs. 4 per unit respectively. One unit of the food A contains 200 units of vitamins, 1 unit of minerals and 40 units of calories, while one unit of the food B contains 100 units of vitamins, 2 units of minerals and 40 units of calories. Find what combination of the foods A and B should be used to have least cost, but it must satisfy the requirements of the sick person. Form the question as L.P.P. and solve it graphically.

Let x units of food A and y units of food B be used where x ≥ 0, y ≥ 0.
Let z be the total cost.
Table

Food	Weight	Vitamins	Minerals	Calories	Cost (Rs.)
A	x	200x	x	40x	5x
B	y	100y	2y	40y	4y
Total		200x + 100y	x + 2 y	40x + 40y	5x + 4y

We are to minimise
z = 5x + 4y
subject to the constraints
200x + 100y ≥ 4000 i.e. 2x + y ≥ 40
x + 2y ≥ 50
40x + 40y ≥ 1400 i.e. x + y ≥ 35
x ≥ 0, y ≥ 0
Consider a set of rectangular cartesian axes OXY in the plane.
It is clear that any point which satisfies x ≥ 0, y ≥ 0 lies in the first quadrant.
Now we draw the graph of 2 x + y = 40
For x = 0, y = 40
For y = 0, 2 x = 40 or x = 20
∴ line meets OX in A(20, 0) and OY in L(0, 40).
Again we draw the graph of
x + 2y = 50
For x = 0, 2y = 50 or y = 25
For y = 0, x = 50
∴ line meets OX in B(50, 0) and OY in M(0, 25).
Again we draw the graph of
x + y = 35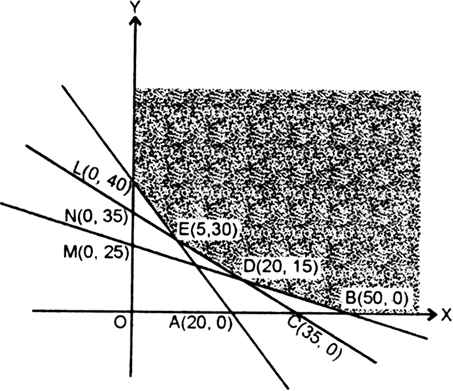

For x = 0, y = 35
For y = 0, x = 35
∴ line meets OX in C(35, 0) and OY in N(0, 35).
Since feasible region satisfies all the constraints.
∴ shaded region is the feasible region, which is unbounded , and corner points are B(50, 0), D(20, 15), E(5, 30), L(0, 40).
At B(50, 0), z = 5(50) + 4(0) = 250 + 0 = 250
At D(20, 15), z = 5(20) + 4(15) = 100 + 60 = 160
At E(5, 30), z = 5(5) + 4(30) = 25 + 120 = 145
At L(0, 40), z = 5(0) + 4(40) = 0 + 160 = 160
∴ least cost = Rs. 145 at (5, 30)
Since feasible region is unbounded.
∴ we are to check whether this cost is minimum.
For this we draw the graph of
5x + 4y < 145 ...(1)
Since (1) has no common point with feasible region.
∴ minimum cost = Rs. 145 at (5, 30)
∴ minimum cost is Rs. 145 when 5 units of food A and 30 units of food B are used.

612 Views

36. Two tailors A and B are paid Rs. 150 and Rs. 200 per day respectively. A can stitch 6 shirts and 4 pants while B can stitch 10 shirts and 4 pants per day. Form a linear programming problem to minimise the labour cost to produce at least 60 shirts and 32 pants. Solve the problem graphically.

353 Views

37. A dietician wishes to mix two types of foods in such a way that vitamin contents of the mixture contain atleast 8 units of vitamin A and 10 units of vitamin C. Food ‘I’ contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C. Food ‘II’ contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C. It costs Rs. 50 per kg to purchase Food ‘I’ and Rs 70 per kg to purchase Food ‘II’. Formulate this problem as a linear programming problem to minimise the cost of such a mixture.

126 Views

38. There two types of fertilisers F₁ and F₂. F₁ consists of 10% nitrogen and 6% phosphoric acid and F₂ consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds that she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F₁ costs Rs 6/ kg and F₂ costs Rs 5/kg, determine how much of each type of fertiliser should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost?

109 Views

39. Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 11 units of vitamin B. Food P costs Rs 60/kg and Food Q costs Rs 80/kg. Food P contains 3 units/kg of Vitamin A and 5 units/kg of Vitamin B while food Q contains 4 units/kg of Vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.

95 Views

40.

A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F₁ and F₂ are available. Food F₁ costs Rs 4 per unit food and F₂ costs Rs 6 per unit. One unit of food F₂ contains 3 units of vitamin A and 4 units of minerals. One unit of food F₂ contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem. Find the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.

135 Views