 Long Answer Type
Long Answer TypeA dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg. food are given below:
|
Food |
Vitamin A |
Vitamin B |
Vitamin C |
|
X |
1 |
2 |
3 |
|
Y |
2 |
2 |
1 |
One kg of food X costs Rs 16 and one kg of food Y costs Rs 20. Find the least cost of the mixture which will produce the required diet?
A retired person wants to invest an amount of Rs. 50, 000. His broker recommends investing in two type of bonds ‘A’ and ‘B’ yielding 10% and 9% return respectively on the invested amount. He decides to invest at least Rs. 20,000 in bond ‘A’ and at least Rs. 10,000 in bond ‘B’. He also wants to invest at least as much in bond ‘A’ as in bond ‘B’. Solve this linear programming problem graphically to maximise his returns.
Maximize Z = 0.1x + 0.09 y
x + y ≤ 50000
x ≥ 20000
y ≥ 10000
y ≤ x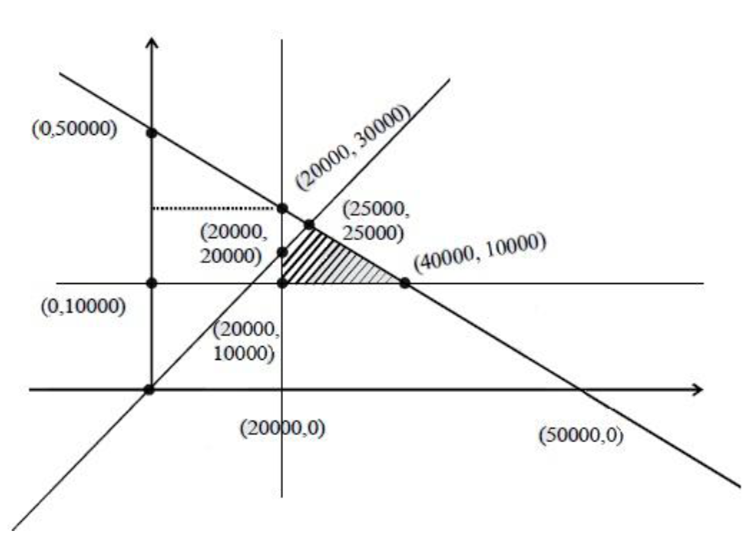
|
|
z=0.1 x+0.09y |
|
P1 (20000,10000) |
2900 |
|
P2(40000,10000) |
4900 |
|
P3(25000,25000) |
4750 |
|
P4(20000,20000) |
3800 |
Minimum and maximum z = 5x + 2y subject to the following constraints:
x – 2y ≤ 2
3x + 2y ≤ 12
−3x + 2y ≤ 3
x ≥ 0, y ≥ 0
A cooperative society of farmers has 50 hectares of land to grow two crops A and B. The profits from crops A and B per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. To control weeds, a liquid herbicide has to be used for crops A and B at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. Keeping in mind that the protection of fish and other wildlife is more important than earning profit, how much land should be allocated to each crop so as to maximize the total profit? Form an LPP from the above and solve it graphically. Do you agree with the message that the protection of wildlife is utmost necessary to preserve the balance in environment?
 Short Answer Type
Short Answer TypeA small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is ` 100 and that on a bracelet is ` 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit? It is being given that at least one of each must be produced.
Solve the following L.P.P. graphically :
Minimise Z = 5x + 10y
Subject to x + 2y ≤ 120
Constraints x + y ≥ 60
x – 2y ≥ 0
and x, y ≥ 0
 Long Answer Type
Long Answer TypeA factory manufactures two types of screws A and B, each type requiring the use of two machines, an automatic and a hand - operated. It takes 4 minutes on the automatic and 6 minutes on the hand-operated machines to manufacture a packet of screws ‘B’. Each machine is available for at most 4 hours on any day. The manufacturer can sell a packet of screws ‘A’ at a profit of 70 paise and screws ‘B’ at a profit of Rs. 1. Assuming that he can sell all the screws he manufactures, how many packets of each type should the factory owner produce in a day in order to maximize his profit? Formulate the above LPP and solve it graphically and find the maximum profit.
A factory owner purchases two types of machines, A and B for his factory. The requirements and the limitations for the machines are as follows:
| Machine | Area occupied | Labour force | daily output ( in units ) |
| A | 1000 m2 | 12 men men | 60 |
| B | 1200 m2 | 8 men | 40 |
He has maximum area of 9000 m2 available, and 72 skilled labourers who can operate both the machines. How many machines of each type should he buy to maximise the daily output?
A diet is to contain at least 80 units of Vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 cost Rs. 4 per unit and F2 costs Rs. 6 per unit. One unit of food F1 contains 3 units of Vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of Vitamin A and 3 units of minerals. Formulate this as a linear programming problem and find graphically the minimum cost for diet that consists of mixture of these two foods and also meets the minerals nutritional requirements.
