 Long Answer Type
Long Answer TypeA small firm manufactures gold rings and chains. The total number of rings and chains manufactured per day is at most 24. It takes 1 hour to make a ring and 30 minutes to make a chain. The maximum number of hours available per day is 16. If the profit on a ring is Rs. 300 and that on a chain is Rs. 190, find the number of rings and chains that should be manufactured per day, so as to earn the maximum profit. Make it as an L.P.P. and solve it graphically
Let x be number of gold rings and y be number of chains manufactured
L.P.P. is
Max Z = 3000 x + 190 y
Substitute in x + y 24
Feasible region
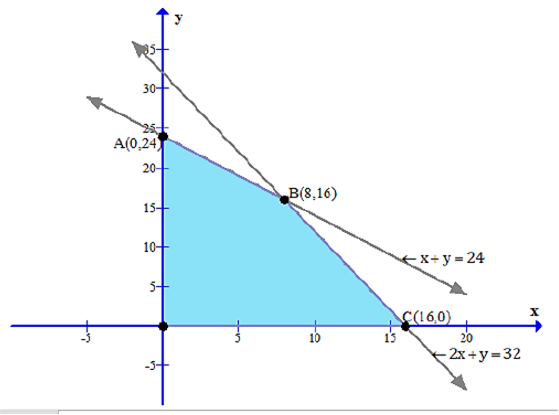
| Corner points |
Value of Z = 300x 190y |
|
| A ( 0, 24 ) | 4560 | |
| B ( 8, 16 ) | 5440 | Maximum |
| C ( 16, 0 ) | 4800 | |
| O ( 0, 0 ) | 0 |
Hence to make the maximum profit, 8 gold rings and 16 chains must be manufactured.
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftsman’s time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftsman’s time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsman’s time. If the profit on a racket and on a bat is Rs20 and Rs 10 respectively, find the number of tennis rackets and crickets bats that the factory must manufacture to earn the maximum profit. Make it as an L.P.P and solve graphically.
A manufacturer produces nuts and bolts. It takes 1 hours of work on machine A and 3 hours on machine B to product a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of `17.50 per package on nuts and `7 per package of bolts. How many packages of each should be produced each day so as to maximize his profits if he operates his machines for at the most 12 hours a day? From the above as a linear programming problem and solve it graphically.
 Multiple Choice Questions
Multiple Choice QuestionsThe line L1: y = x = 0 and L2: 2x + y = 0 intersect the line L3: y + 2 = 0 at P and Q respectively. The bisectorof the acute angle between L1 and L2 intersects L3 at R.
Statement-1: The ratio PR: RQ equals 2√2:√5
Statement-2: In any triangle, the bisector of an angle divides the triangle into two similar triangles.
Statement-1 is true, Statement-2 is true ; Statement-2 is correct explanation for Statement-1
Statement-1 is true, Statement-2 is true ; Statement-2 is not a correct explanation for Statement-1
Statement-1 is true, Statement-2 is false
Statement-1 is true, Statement-2 is false
For the LPP Min z = x1 + x2 such that inequalities 5x1 + 10x2 0, x1 + x2 1, x2 4 and x1, x2 > 0
There is a bounded solution
There is no solution
There are infinite solutions
None of these
The maximum value of the objective function Z = 3x + 2y for linear constraints x + y 7, 2x + 3y 16, x2 0, y2 0 is
16
21
25
28
A diet of a sick person must contain atleast 4000 unit of vitamins, 50 unit of proteins and 1400 calories. Two foods A and B are available at cost rs. 4 and rs. 3 per unit respectively. If one unit of A contains 200 unit of vitamins, 1 unit of protein and 40 calories, while one unit of food B contains 100 unit of vitamins, 2 unit of protein and 40 calories. Formulate the problem, so that the diet be cheapest
None of the above
