355.
If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 - 2x + k, the remainder comes out to be x + a, find ‘k’ and ‘a’.
By division algorithm, we have It is given that f(a) = x4 – 6x3 + 16x2 – 25x + 10, when divided by x2 – 2x + k leaves x + a as remainder.
:. f(x) – (x + a) = x4 – 6x3 + 16x2–26x + 10 – a is is exactly divisible by x2 – 2x + k.
Let us now divide x4 – 6x3 + 16x2 – 26x + 10 – a by x2 – 2x + k.
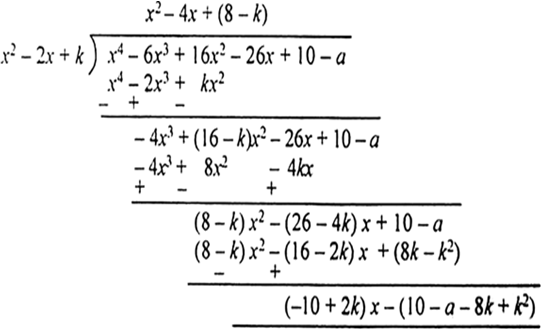
For f(x) – (x + a) = x4 – 6x3 + 16x2 – 26x + 10 – a to be exactly divisible by x2 – 2x + k, we must have
(–10 + 2k) x + (10 – a – 8k + k2) = 0 for all x
⇒ – 10 + 2k = 0, 10 – a – 8k + k2 = 0
⇒ k = 5, 10 – a – 40 + 25 = 0
⇒ k = 5 and a = – 5.
2902 Views
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type
 Short Answer Type
Short Answer Type