 Short Answer Type
Short Answer TypeA die is thrown once. Find the probability of getting
(i) an odd number.
(ii) a number greater than 4.
(iii) seven.
A pair of dice is thrown once. Find the probability of getting a total of 5 on two dice.
When a pair of dice is thrown once then possible outcome(s) are 36. i.e., n( S) = 36
Let A be the favourable outcomes of getting the same number of each dice, then
S= ((1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2.1), (2,2), (2,3), (2,4), (2,5), (2,6)
(3.1), (3,2), (3,3), (3,4), (3,5), (3,6)
(4.1), (4,2), (4,3), (4,4), (4,5), (4,6)
(5.1), (5,2), (5,3), (5,4), (5,5), (5,6)
(6.1), (6,2), (6,3), (6,4), (6,5), (6,6)}
⇒ (A) = {(11), (2,2), (3,3), (4,4), (5,5), (6,6))
i.e. n( A)= 6
Therefore,![]()
Two dice are thrown simultaneously. What is the probability that
(i) 5 will not come up on either of them?
(ii) 5 will come up on at least one?
(iii) 5 will come at both dice?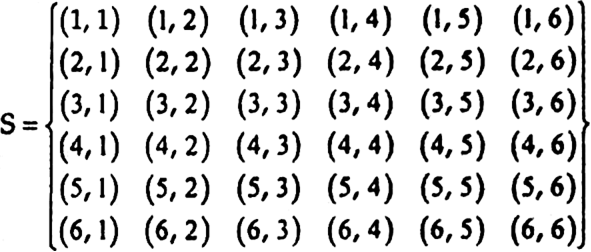
Two dice are thrown simultaneously. Find the probability of getting :
(i) a sum less than 6 (ii) a sum less than 7
(iii) a sum more than 7 (iv) 8 as the sum
A card is drawn from a pack of 52 playing cards. What is the probability that it is
(i) an ace
(ii) a face card
(iii) any card numbered from 2 to 10?
One card is drawn from a pack of 52 cards, each of the 52 cards being equally likely to be drawn. Find the probability that the card drawn is :
(i) red (ii) either red or king
(iii) red and a king (iv) a red face card
(v) ‘2’ of spades (vi) ‘10’ of a black suit.
