 Long Answer Type
Long Answer TypeHere n = 50
![]()
(a) P(at least once) = 1 - P(0) = ![]()
(b) P(exactly once) = P(1) = ![]()
![]()
(c) P(at least twice) = 1 - [P(0) + P(1)]
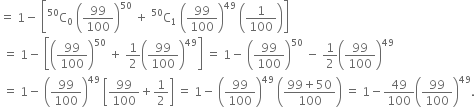
An urn contains 25 balls of which 10 balls bear a mark ‘X’ and the remaining 15 bear a mark ‘Y’ . A ball is drawn at random and it is replaced. If 6 balls are drawn in this way, find the probability that
(i) all will bear mark X
(ii) not more than 2 balls will bear 'Y' mark.
(iii) at least one ball will bear 'Y' mark.
(iv) the number of balls with 'X' mark and 'Y' mark will be equal.
 Short Answer Type
Short Answer Type Multiple Choice Questions
Multiple Choice Questions Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeA bag X contains 4 white balls and 2 black balls, while another bag Y contains 3 white balls and 3 black balls. Two balls are drawn (without replacement) at random from one of the bags and were found to be one white and one black. Find the probability that the balls were drawn from bag Y.
