Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Probability

Long Answer Type

1071. If a fair coin is tossed 10 times, find the probability of
(i) exactly six heads
(ii) at least six heads
(iii) at most six heads

106 Views

1072. A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is

1 over 100.

What is the probaility that he will win a prize exactly once (a) at least once (b) exactly once (c) at least twice?

94 Views

1073.
An urn contains 25 balls of which 10 balls bear a mark ‘X’ and the remaining 15 bear a mark ‘Y’ . A ball is drawn at random and it is replaced. If 6 balls are drawn in this way, find the probability that
(i) all will bear mark X
(ii) not more than 2 balls will bear 'Y' mark.
(iii) at least one ball will bear 'Y' mark.
(iv) the number of balls with 'X' mark and 'Y' mark will be equal.

Here n = 6
p = (Probability that a ball marked 'X' is drawn) = $10 over 25 space equals space 2 over 5$

$therefore space space space straight q space equals space straight P left parenthesis straight a space ball space marked space straight Y space is space drawn right parenthesis space equals space 1 space minus space straight p space equals space 1 minus 2 over 5 space equals space 3 over 5$

(i) P(all balls bear X mark) = P(6) = $straight C presuperscript 6 subscript 6 space open parentheses 3 over 5 close parentheses to the power of 6 minus 6 end exponent space open parentheses 2 over 5 close parentheses to the power of 6 space equals space open parentheses 2 over 5 close parentheses to the power of 6$
(ii) P(not more than 2 will bear Y mark)
= P(not less than 4 will bear X mark) = P(4) + P(5) + P(6)
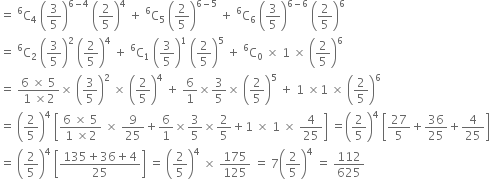
$equals space straight C presuperscript 6 subscript 4 space open parentheses 3 over 5 close parentheses to the power of 6 minus 4 end exponent space open parentheses 2 over 5 close parentheses to the power of 4 space plus space straight C presuperscript 6 subscript 5 space open parentheses 2 over 5 close parentheses to the power of 6 minus 5 end exponent space plus space straight C presuperscript 6 subscript 6 space open parentheses 3 over 5 close parentheses to the power of 6 minus 6 end exponent space open parentheses 2 over 5 close parentheses to the power of 6 equals space straight C presuperscript 6 subscript 2 space open parentheses 3 over 5 close parentheses squared space open parentheses 2 over 5 close parentheses to the power of 4 space plus space straight C presuperscript 6 subscript 1 space open parentheses 3 over 5 close parentheses to the power of 1 space open parentheses 2 over 5 close parentheses to the power of 5 space plus space straight C presuperscript 6 subscript 0 space cross times space 1 space cross times space open parentheses 2 over 5 close parentheses to the power of 6 equals space fraction numerator 6 space cross times space 5 over denominator 1 space cross times 2 end fraction cross times space open parentheses 3 over 5 close parentheses squared space cross times space open parentheses 2 over 5 close parentheses to the power of 4 space plus space 6 over 1 cross times 3 over 5 cross times space open parentheses 2 over 5 close parentheses to the power of 5 space plus space 1 space cross times 1 space cross times space open parentheses 2 over 5 close parentheses to the power of 6 equals space open parentheses 2 over 5 close parentheses to the power of 4 space open square brackets fraction numerator 6 space cross times space 5 over denominator 1 space cross times 2 end fraction space cross times space 9 over 25 plus 6 over 1 cross times 3 over 5 cross times 2 over 5 plus 1 space cross times space 1 space cross times space 4 over 25 close square brackets space equals open parentheses 2 over 5 close parentheses to the power of 4 space open square brackets 27 over 5 plus 36 over 25 plus 4 over 25 close square brackets equals space open parentheses 2 over 5 close parentheses to the power of 4 space open square brackets fraction numerator 135 plus 36 plus 4 over denominator 25 end fraction close square brackets space equals space open parentheses 2 over 5 close parentheses to the power of 4 space cross times space 175 over 125 space equals space 7 open parentheses 2 over 5 close parentheses to the power of 4 space equals space 112 over 625$
(iii) P(number of balls with X mark and Y mark equal)
   $equals space straight P left parenthesis 3 right parenthesis space equals space straight C presuperscript 6 subscript 3 space open parentheses 3 over 5 close parentheses to the power of 6 minus 3 end exponent space open parentheses 2 over 5 close parentheses cubed space equals space fraction numerator 6 space cross times space 5 space cross times space 4 over denominator 1 space cross times space 2 space cross times space 3 end fraction cross times space open parentheses 3 over 5 close parentheses cubed space open parentheses 2 over 5 close parentheses cubed space equals space 20 space cross times space open parentheses 3 over 5 close parentheses cubed space cross times space open parentheses 2 over 5 close parentheses cubed$
(iv) P(at least one ball bear Y mark)
= P(not more than 5 balls bear mark X)
   $equals space 1 minus straight P left parenthesis 6 right parenthesis space equals space 1 space minus space open parentheses 2 over 5 close parentheses to the power of 6.$ $open square brackets because of space left parenthesis straight i right parenthesis close square brackets$

104 Views

Short Answer Type

1074. In an examination, 20 questions of true-false type are asked. Suppose a student tosses a fair coin to determine his answer to each question. If the coin falls heads, he answers ‘true’ ; if it falls tails, he answers ‘false’. Find the probability that he answers at least 12 questions correctly.

148 Views

1075. Suppose that 90% of people are right-handed. What is the probability that at most 6 of a random sample of 10 people are right-handed?

89 Views

1076. How many times must a man toss a fair coin so that the probability of having at least one head is more than 90%?

139 Views

Multiple Choice Questions

1077. In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is

$10 to the power of negative 1 end exponent$
$open parentheses 1 half close parentheses to the power of 5$
$open parentheses 9 over 10 close parentheses to the power of 5$
$open parentheses 9 over 10 close parentheses to the power of 5$

114 Views

1078. The probability that a student is not a swimmer is

1 fifth.

Then the probability that out of five students, four are swimmers is

$straight C presuperscript 5 subscript 4 space open parentheses 4 over 5 close parentheses to the power of 4 space 1 fifth$
$open parentheses 4 over 5 close parentheses to the power of 4 space 1 fifth$
$straight C presuperscript 5 subscript 1 space open parentheses 4 over 5 close parentheses to the power of 4$
$straight C presuperscript 5 subscript 1 space open parentheses 4 over 5 close parentheses to the power of 4$

87 Views

Long Answer Type

1079. A and B throw two dice simultaneously turn by turn. A will win if he throws a total of 5, B will win if he throws a doublet. Find the probability that B will win the game, though A started the game.

176 Views

Short Answer Type

1080.

A bag X contains 4 white balls and 2 black balls, while another bag Y contains 3 white balls and 3 black balls. Two balls are drawn (without replacement) at random from one of the bags and were found to be one white and one black. Find the probability that the balls were drawn from bag Y.

1714 Views