Short Answer Type
Short Answer TypeGiven: ABCD is a rectangle with
∠A = 90°.
To Prove: ∠A = ∠B = ∠C = ∠D = 90°
Proof: ∵ ABCD is a rectangle
∴ ABCD is a parallelogram
∴ AD || BC
| Opposite sides of a parallelogram are
parallel
and transversal AB intersects them
∴ ∠A + ∠B = 180°
| Sum of the consecutive interior angles on the same side of a transversal is 180°
⇒ 90° + ∠B = 180° | ∵ ∠A = 90° (given)
⇒ ∠B = 90°
Similarly, we can show that
∠C = 90° and ∠D = 90°
Hence, ∠A = ∠B = ∠C = ∠D = 90°.
In a quadrilateral ABCD, the line segments bisecting ∠C and ∠D meet at E.
Prove that ∠A + ∠B = 2 ∠CED
ABC is an isosceles triangle in which AB = AC. AD bisects ∠PAC and CD || AB. Show that
(i) ∠DAC = ∠BCA
(ii) ABCD is a parallelogram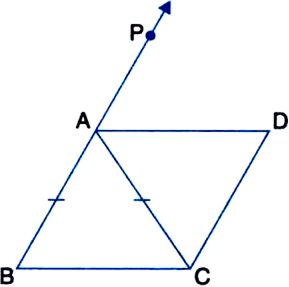
ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle ∠PAC and CD || AB (see figure). Show that:
(i) ∠DAC = ∠BCA and
(ii) ABCD is a parallelogram.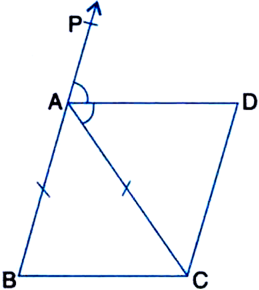
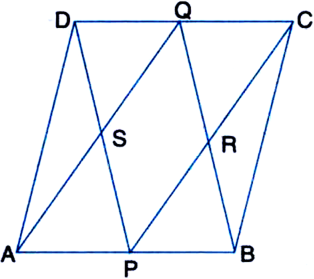
ABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:
(i) APCQ is a parallelogram.
(ii) DPBQ is a parallelogram.
(iii) PSQR is a parallelogram.