Short Answer Type
Short Answer Type
The angles A, B, C and D of a quadrilateral have measures in the ratio 2 : 4 : 5 : 7. Find the measures of these angles. What type of quadrilateral is it? Give reasons.
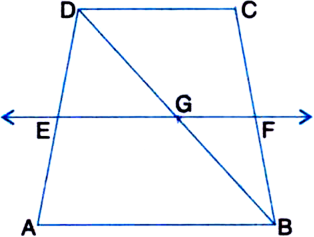
In the figure, ABCD is a parallelogram in which AB is produced to E so that AB = BE
(a) Prove that ED bisects BC
(b) If AD = 10 cm, find OB.
 Long Answer Type
Long Answer Type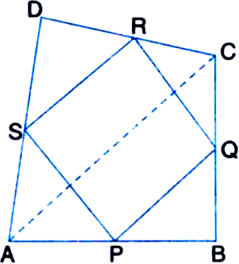
 Short Answer Type
Short Answer TypeGiven: ABCD is a rhombus. P, Q, R, S are the mid-points of AB, BC, CD, DA respectively. PQ, QR, RS and SP are joined.
To Prove: PQRS is a rectangle.
Construction: Join AC and BD.
Proof: In triangles RDS and PBQ,
DS = QB
| Halves of opposite sides of || gm ABCD which are equal
DR = PB
| Halves of opposite sides of || gm ABCD which are equal
∠SDR = ∠QBP
| Opposite ∠s of ||gm ABCD which are equal
∴ ∆RDS = ∆PBQ
| SAS Congruence Axiom
∴ SR = PQ | C.P.C.T.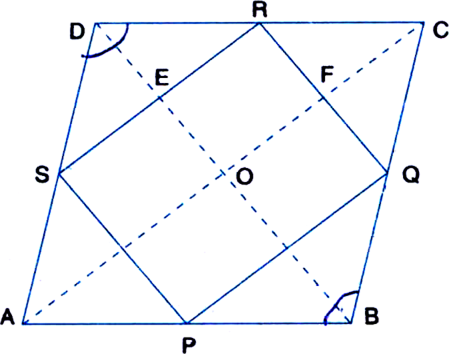
In triangles RCQ and PAS,
RC = AP
| Halves of opposite sides of || gm ABCD which are equal
CQ = AS
Halves of opposite sides of || gm ABCD which are equal
∠RCQ = ∠PAS
Opposite ∠s of || gm ABCD which are equal
∴ ∆RCQ ≅ ∆PAS
| SAS Congruence Axiom
∴ RQ = SP | C.P.C.T.
∴ In PQRS,
SR = PQ and RQ = SP
∴ PQRS is a parallelogram,
In ∆CDB,
∵ R and Q are the mid-points of DC and CB respectively.
∴ RQ || DB ⇒ RF || EO.
Similarly, RE || FO
∴ OFRE is a || gm
∴ ∠R = ∠EOF = 90°
| ∵ Opposite ∠s of a || gm are equal and diagonals of a rhombus intersect at 90°
Thus PQRS is a rectangle.