Long Answer TypeThe following table shows the ages of the patients admitted in a hospital during a year.
Find the mode and mean of the data given below. Compare and interpret the measures of central tendency.
|
Age (in yrs) |
No. of patients |
|
5-15 |
6 |
|
15-25 |
11 |
|
25-35 |
21 |
|
35-45 |
23 |
|
45-55 |
14 |
|
55-65 |
5 |
Short Answer TypeThe following data gives the information on the observed life-times (in hours) of 225 electrical components.
|
Life time (in hours) |
Frequency |
|
0-20 |
10 |
|
20-40 |
35 |
|
40-60 |
52 |
|
60-80 |
61 |
|
80-100 |
38 |
|
100-120 |
29 |
Determine the modal lifetimes of the components.
Long Answer TypeThe following data gives the distribution of total monthly household expenditure of 200 families of a village. Find the modal monthly expenditure of the families. Also, find the mean monthly expenditure:
|
Expenditure (in Rs.) |
Number of families |
|
1000-1500 |
24 |
|
1500-2000 |
40 |
|
2000-2500 |
33 |
|
2500-3000 |
28 |
|
3000-3500 |
30 |
|
3500-4000 |
22 |
|
4000-4500 |
16 |
|
4500-5000 |
7 |
Short Answer TypeThe following distribution gives the state-wise teacher-student ratio in higher secondary schools of India. Find the mode and mean of this data. Interpret the two measures.
|
Number of students per teacher |
Number of states/U.T. |
|
15-20 |
3 |
|
20-25 |
8 |
|
25-30 |
9 |
|
30-35 |
10 |
|
35-40 |
3 |
|
40-45 |
0 |
|
45-50 |
0 |
|
50-55 |
2 |
The given distribution shows the number of runs scored by some top batsmen of the world in one-day international cricket matches.
|
Runs scored |
Number of batsman |
|
3000-4000 |
4 |
|
4000-5000 |
18 |
|
5000-6000 |
9 |
|
6000-7000 |
7 |
|
7000-8000 |
6 |
|
8000-9000 |
3 |
|
9000-10000 |
1 |
|
10000-11000 |
1 |
|
Runs scored |
Number of batsman |
|
3000-4000 |
4 |
|
4000-5000 |
18 |
|
5000-6000 |
9 |
|
6000-7000 |
7 |
|
7000-8000 |
6 |
|
8000-9000 |
3 |
|
9000-10000 |
1 |
|
10000-11000 |
1 |
Here, maximum class frequency is 18 and the class corresponding to frequency is 4000-5000. So, the modal class = 4000-5000.
Now,
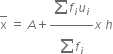
Thus, we have Modal class = 4000-5000, l = 4000, f1 = 18, f0 = 4, f2 = 9 and h = 1000
Now, substituting these values in the formula of mode, we get
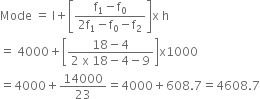
A student noted the number of cars passing through a spot on a road for 100 periods each of 3 minutes and summarised it in the table given below. Find the mode of the data :
|
Numberof cars |
0-10 |
10-20 |
20-30 |
30-40 |
40-50 |
50-60 |
60-70 |
70-80 |
|
Frequency |
7 |
14 |
13 |
12 |
20 |
11 |
15 |
8 |
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them.
|
Monthly consumption of electricity (in units) |
Number of consumers |
|
68-85 |
4 |
|
85-105 |
5 |
|
105-125 |
13 |
|
125-145 |
20 |
|
145-165 |
14 |
|
165-185 |
8 |
|
185-205 |
4 |
If the median of the distribution given below is 28.5, find the values of x and y.
|
Class interval |
Frequency |
|
0-10 |
5 |
|
10-20 |
x |
|
20-30 |
20 |
|
30-40 |
15 |
|
40-50 |
y |
|
50-60 |
5 |
|
Total |
x = 60 |
A life insurance agent found the folio wing data for distribution of ages of 100 policy holders. Calculate the median age, if policies are only given to persons having age 18 yrs. onwards but less than 60 years.
|
Age (in yrs.) |
No. of policy holders |
|
below 20 |
2 |
|
below 25 |
6 |
|
below 30 |
24 |
|
below 35 |
45 |
|
below 40 |
78 |
|
below 45 |
89 |
|
below 50 |
92 |
|
below 55 |
98 |
|
below 60 |
100 |
The lengths of 40 leaves of a plant are measured correct to the nearest millimetre and the data obtained is represented in the following table:
|
Length (in nun) |
Number of leaves |
|
118-126 |
3 |
|
127-135 |
5 |
|
136-144 |
9 |
|
145-153 |
12 |
|
154-162 |
5 |
|
163-171 |
4 |
|
172-180 |
2 |
Find the median length of the leaves.
Switch
