Long Answer TypeA survey regarding the heights (in cm) of 50 girls of class X of a school was conducted and the following data was obtained:
|
Height in cm |
120 - 130 |
130 - 140 |
140 - 150 |
150 - 160 |
160 - 170 |
Total |
|
Number of girls |
2 |
8 |
12 |
20 |
8 |
50 |
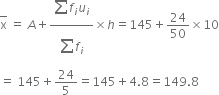
Finding Median:
|
Class Interval |
Frequency (f1) |
Cf |
|
120 - 130 |
2 |
2 |
|
130 - 140 |
8 |
10 |
|
140 - 150 |
12 |
22 |
|
150 - 160 |
20 |
42 |
|
160 - 170 |
8 |
50 |
observationwhich lies in the class 150-160
Thus we have
Median class = 150 - 160
l = 150, 
, h = 10, cf = 22 and f = 20
Putting these values in the formula of Median, we get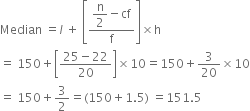
III. Finding Mode
|
Class Interval |
No. of Students (f) |
|
120 - 130 |
2 |
|
130 - 140 |
8 |
|
140 - 150 |
12 |
|
150 - 160 |
20 |
|
160 - 170 |
8 |
Here, the man class frequency is 20 and the class corresponding to frequency is 150 - 160, So, the modal class is 150 - 160.
Thus, we have
Modal class = 150-160
l = 150,f1 = 20
f0 = 12, f2 = 8, n = 10
Now,
Substituting these values in the formula of made, we get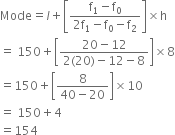
Find mean, median and mode of the following data:
|
Classes |
Frequency |
|
0-20 |
6 |
|
20-40 |
8 |
|
40-60 |
10 |
|
60-80 |
12 |
|
80-100 |
6 |
|
100-120 |
5 |
|
120-140 |
3 |
Find mean, median and mode of the following data:
|
Classes |
Frequency |
|
0 - 50 |
2 |
|
50 - 100 |
3 |
|
100 - 150 |
5 |
|
150 - 200 |
6 |
|
200 - 250 |
5 |
|
250 - 300 |
3 |
|
300 - 350 |
1 |
The following table gives the daily income of 50 workers of a factory :
|
Daily income (in Rs.) |
No. of Workers |
|
100-120 |
12 |
|
120-140 |
14 |
|
140-160 |
8 |
|
160-180 |
6 |
|
180-200 |
10 |
Find the Mean, Mode and Median of the above data.
Short Answer TypeFind the mode, median and mean for the following data :
|
Marks Obtained |
Number of Students |
|
25-35 |
7 |
|
35-45 |
31 |
|
45-55 |
33 |
|
55-65 |
17 |
|
65-75 |
11 |
|
75-85 |
1 |
Long Answer TypeThe table given below shows the frequency distribution of the scores obtained by 200 candidates in a BCA examination.
|
Score |
No. of candidates |
|
200-250 |
30 |
|
250-300 |
15 |
|
300-350 |
45 |
|
350-400 |
20 |
|
400-450 |
25 |
|
450-500 |
40 |
|
500-550 |
10 |
|
550-600 |
15 |
Draw cumulative frequency curves by using (i) 'less than series', (ii) 'more than series'.
Draw both types of cumulative freqneucy curve on the same graph paper and then determine the median.
|
Marks obtained |
No. of students |
|
50-60 |
4 |
|
60-70 |
8 |
|
70-80 |
12 |
|
80-90 |
6 |
|
90-100 |
6 |
Draw 'less than' and 'more than' ogive curve from the following and indicate the value of median.
|
Marks |
No. of students (f) |
|
0-5 |
7 |
|
5-10 |
10 |
|
10-15 |
20 |
|
15-20 |
13 |
|
20-25 |
12 |
|
25-30 |
10 |
|
30-35 |
14 |
|
35-40 |
9 |
|
Daily Income (in Rs.) |
Number of Workers |
|
100-120 |
12 |
|
120-140 |
14 |
|
140-160 |
8 |
|
160-180 |
6 |
|
180-200 |
10 |
During the medical check-up of 35 students of a class their weights were recorded as follows:
|
Weight (in kg.) |
No. of Students |
|
38—40 |
3 |
|
40—42 |
2 |
|
42—44 |
4 |
|
44—46 |
5 |
|
46—48 |
14 |
|
48—50 |
4 |
|
50—52 |
3 |
Draw a less than type and a more than type ogive from the given data. Hence obtain the median weight from the graph.
Switch
