Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Statistics

Long Answer Type

291.

A survey regarding the heights (in cm) of 50 girls of class X of a school was conducted and the following data was obtained:

Height in cm	120 - 130	130 - 140	140 - 150	150 - 160	160 - 170	Total
Number of girls	2	8	12	20	8	50

1558 Views

292.

Find mean, median and mode of the following data:

Classes	Frequency
0-20	6
20-40	8
40-60	10
60-80	12
80-100	6
100-120	5
120-140	3

Median space equals space straight l plus open parentheses fraction numerator begin display style straight N over 2 end style minus straight c. straight f. over denominator straight f end fraction close parentheses cross times straight h equals 60 plus fraction numerator 25 minus 24 over denominator 12 end fraction cross times 20 equals 60 plus 20 over 12 equals space 60 plus 5 over 3 equals 60 plus 1.67 equals 61.67

642 Views

293.

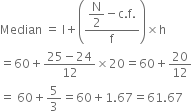
Find mean, median and mode of the following data:

Classes	Frequency
0 - 50	2
50 - 100	3
100 - 150	5
150 - 200	6
200 - 250	5
250 - 300	3
300 - 350	1

977 Views

294.

The following table gives the daily income of 50 workers of a factory :

Daily income (in Rs.)	No. of Workers
100-120	12
120-140	14
140-160	8
160-180	6
180-200	10

Find the Mean, Mode and Median of the above data.

1455 Views

Short Answer Type

295.

Find the mode, median and mean for the following data :

Marks Obtained	Number of Students
25-35	7
35-45	31
45-55	33
55-65	17
65-75	11
75-85	1

197 Views

Long Answer Type

296.
The table given below shows the frequency distribution of the scores obtained by 200 candidates in a BCA examination.

Score

No. of candidates

200-250

30

250-300

15

300-350

45

350-400

20

400-450

25

450-500

40

500-550

10

550-600

15

Draw cumulative frequency curves by using (i) 'less than series', (ii) 'more than series'.

e assume a class interval 150-200 prior to the first class interval 200-250 wtih zero frequency.
Cumulative frequency distribution [Less than Series]

Scroe	c.f.
Less than 200	0
Less than 250	30
Less than 300	45
Less than 350	90
Less than 400	110
Less than 450	135
Less than 500	175
Less than 550	185
Less than 600	200

Now, we plot the points : (200, 0), (250, 30), (300, 45), (350, 90), (400, 110), (450, 135), (500, 175), (550, 185), (600, 200).

e assume a class interval 150-200 prior to the first class interval 2

e assume a class interval 150-200 prior to the first class interval 2

More than Series

Scroe	c.f.
More than 200	200
More than 250	170
More than 300	155
More than 350	110
More than 400	90
More than 450	65
More than 500	25
More than 550	15
More than 600	0

Now, we plot the pts.: (200, 200), (250,170), (300,155), (350,110), (400, 90), (450, 65), (500, 25), (550, 15) and (600, 0).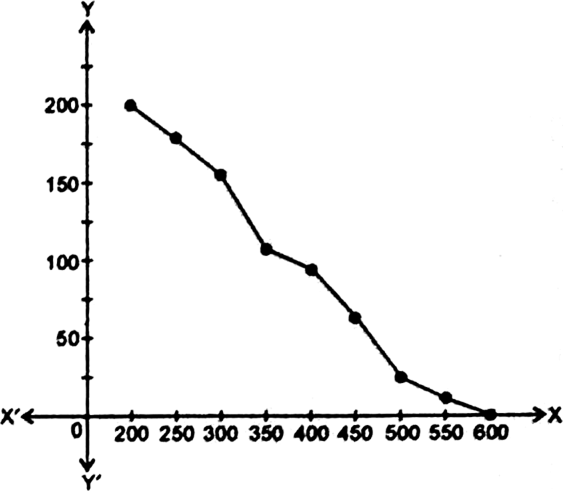

e assume a class interval 150-200 prior to the first class interval 2

409 Views

297.

Draw both types of cumulative freqneucy curve on the same graph paper and then determine the median.

Marks obtained	No. of students
50-60	4
60-70	8
70-80	12
80-90	6
90-100	6

190 Views

298.

Draw 'less than' and 'more than' ogive curve from the following and indicate the value of median.

Marks	No. of students (f)
0-5	7
5-10	10
10-15	20
15-20	13
20-25	12
25-30	10
30-35	14
35-40	9

2485 Views

299. The following table gives the daily income of 50 workers of a factory. Draw both types ("less than type" and "greater than type") ogives and determine the median of the data.

Daily Income (in Rs.)	Number of Workers
100-120	12
120-140	14
140-160	8
160-180	6
180-200	10

1338 Views

300.

During the medical check-up of 35 students of a class their weights were recorded as follows:

Weight (in kg.)	No. of Students
38—40	3
40—42	2
42—44	4
44—46	5
46—48	14
48—50	4
50—52	3

Draw a less than type and a more than type ogive from the given data. Hence obtain the median weight from the graph.

782 Views

Score	No. of candidates
200-250	30
250-300	15
300-350	45
350-400	20
400-450	25
450-500	40
500-550	10
550-600	15